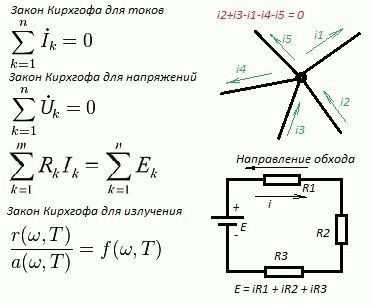
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2:Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.
Здесь ток I1- ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
I1 = I2 + I3 (1)
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим:
I1 — I2 — I3 = 0 (2)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
E1- Е2 = -UR1 — UR2 или E1 = Е2 — UR1 — UR2 (3)
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Законы Кирхгофа в комплексной форме
Итак, для того, чтобы вывести математическую формулировку первого закона в комплексной формуле, необходимо представить все синусоидальные токи в комплексных значениях. Формула примет данный вид:
Комплексная форма первого закона Кирхгофа
Расшифровывая формулу получим, что алгебраическая сумма комплексных значений токов всех ветвей, которые сходятся в узле цепи, будет равняться нулю.
Закон №2 сформулирован не менее просто. Для контура замещения, который содержит лишь неактивные элементы и источники ЭДС, в каждую секунду алгебраическая сумма напряжений на данных элементах контура равняется числовой сумме ЭДС. Некоторым может показаться данная формулировка трудной, но при реальном разборе станет ясно, что все весьма просто и элементарно:
Комплексная форма второго закона Кирхгофа

Например, рассмотрим рисунок. Для выбранного на схеме замещения контура 1
u1-u2-u3+u4=0
Для второго контура:
ur-uL=e1-e2
В комплексной записи закон выглядит таким образом:
Контур 1
Контур 2
Второй закон Кирхгофа: определение
Второй закон вызывает у многих вопросы, так как он несколько труднее первого, но этот миф легко можно развеять, объяснив принцип работы. Для начала необходимо разобрать определение закона, который звучит таким образом: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех пассивных элементах цепи.
Формулировка определения несколько затрудняет его понимание, поэтому можно упростить: сумма ЭДС в замкнутом контуре равняется сумме падений напряжений. Так намного проще и понятнее.
Закон напряжения и формула для магнитной цепи
Формула, которая выражает этот закон, примет такой вид:

Формула второго закон Кирхгофа
В качестве примера возьмём самый элементарный и понятный для всех случай. Нам понадобится взять батарейку и резистор – всё в одном экземпляре. Так как резистор в единичном количестве, так же как и батарейка, то ЭДС батарейки будет равняться 1,5 ватт, и это равно падению напряжения на резисторе.
Если для примера взять уже два резистора и подключить их к батарейке, то 1,5 ватт будут распределяться равномерно на обоих резисторах, то есть на каждом окажется по 0,75 ватт. Если взять уже три резистора по 1 кОм, то падение напряжения будет на них уже по 0,5 ватт. Логика расчётов сохраняется в любом случае. Формула примет вид:
| Формула | Е1 = IR1 + IR2 + IR3 |
| Преобразование | 1,5 Вт = 0,5 Вт + 0,5 Вт + 0,5 Вт |
| Итог | 1,5 Вт = 1,5 Вт |
Важно! Второй закон будет работать независимо от того, сколько использовано источников питания и нагрузок. Не влияет на расчёты и место их расположения в контуре схемы. Так что даже у разных схем решение может быть одинаковым, но должно быть соблюдено условие – количество элементов должно быть идентичным.
Законы Киргофа для электрических цепей
- Первый закон Киргофа гласит, что алгебраическая сумма токов в узле цепи равна нулю. Исходящие токи берутся при вычислениях с отрицательным знаком, входящие – с положительным. Хотя в русскоязычной литературе говорится, что допустимо наоборот. Суть неизменна.
- Второй закон Киргофа формулируется для замкнутых контуров. Утверждает, что сумма падений напряжений при обходе по кругу равна всем встречающимся на пути ЭДС. Причём контуры любой цепи нужно обходить в едином направлении: по или против часовой стрелки.
Первое уравнение не нуждается в пояснении. Порой сложно понять, в каком направлении течёт ток, с отрицательным или положительным знаком требуется подставить в формулу. Рекомендуется помнить: количество уравнений на единицу меньше, нежели узлов. Если присутствуют сомнения по точке, допустимо исключить её из рассмотрения. В прочих ситуациях анализируется знак разницы потенциалов на концах проблемного участка. Для этого складываются или вычитаются действующие здесь источники питания (в задачках по физике – батарейки).
По общепринятым нормам более длинная черта в графическом обозначении аккумулятора считается положительным полюсом. Ток вытекает отсюда по правилам, принятым в физике, хотя на практике все происходит наоборот – движение образовано отрицательно заряженными электронами. Если ЭДС действуют на участке в разных направлениях, они вычитаются, а направление тока задаётся наибольшей.
Что касается второго закона, знак вхождения в формулу падения напряжения на установленном участке определяется направлением протекания тока. ЭДС берутся с противоположным знаком, либо стоят по другую сторону равенства. Как указано выше, ячейки нужно обходить в одном направлении. Не смущайтесь, что в формулах над напряжением и током стоит точка. Это знак комплексного числа.
Обратите внимание – дана упрощённая запись второго закона. Здесь все ЭДС берутся с обратным реально присутствующему на рисунке знаком. Известна иная форма записи, где падения напряжения отделены от ЭДС знаком равенства. Тогда знаки менять не нужно. Последняя форма записи даётся в школьном курсе физики и приведена на рисунке чуть ниже общей.

Правило Кирхгофа
Работы Кирхгофа в области спектроскопии
Кирхгоф и Бунзен активно изучали спектры излучения химических элементов, используя изобретения Фраунгофера. При помощи призмы или дифракционной решётки свет раскладывался на спектральные составляющие, и учёные наблюдали эффект. Так установлены индивидуальные частоты ряда элементов таблицы Менделеева. Указанные учёные заложили основы спектроскопии. В 1860 году опубликованы исследования восьми элементов и их уникальных спектров, среди прочих:
- стронций;
- литий;
- калий;
- кальций;
- барий;
- натрий.
Кирхгоф и Бунзен показали, что можно проводить химический анализ веществ при помощи спектроскопии и открыли элементы, прежде неизвестные в науке (цезий – в Древнем Риме «голубой» по спектру свечения и рубидий – в Древнем Риме «темно-красный»). Установили связь между спектрами излучения и поглощения, на основании характеристик солнечного света показали избранные свойства нашего светила (наличие железа, калия, кальция, магния, никеля, хрома и натрия в атмосфере звезды, отсутствие лития). Опыты требовалось проводить в период близости Солнца к зениту: когда звезда клонилась к горизонту, увеличивался итоговый эффект вклада атмосферы Земли. Как результат работы, на свет появился закон Кирхгофа для термодинамики.
Применяя устройства, разлагающие спектр на составляющие, учёные открыли ряд прочих законов, упомянутых выше. Учёный применял бунзеновскую горелку (Бунзен), в пламя вводил хлористый натрий или хлористый литий. В результате при помощи дифракционной решётки наблюдал дискретный спектр, причём установлено, что поглощение идёт на прежних частотах. Выводы Кирхгофа:
- Раскалённое газообразное тело, образованное в пламени горелки испускает дискретный спектр излучения.
- Установлено, что в солнечном излучении отсутствуют частоты элемента натрия. Учёный сложил дневной свет с пламенем бунзеновой горелки, дефект изгладился. Излучение натрия в лаборатории дополнило спектр Солнца.
- Если потом для опыта бралась спиртовая горелка, тёмные полосы становились чернее. Следовал вывод, что при относительно низкой температуре газообразного тела в пламени горелки оно начинает поглощать. Так установлено, что в более холодной относительно ядра солнечной атмосфере имеется натрий.
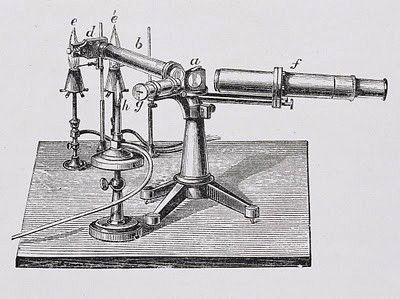

Опыт с горелкой
Лучшей горелкой для опытов учёный считал газовую. Поскольку светимость её пламени низка и не мешает регистрировать спектр газообразного тела. Соли для опытов брались максимально чистыми, производилось многократное осаждение. Для наблюдения использовался чёрный ящик, в стенки устройства под острым углом вставлялись две подзорные трубы:
- через первую наблюдатель лицезрел зачернённую заднюю стенку;
- через вторую свет концентрировался на выбранном участке.
Вращающаяся призма помогала зафиксировать напротив глаз наблюдателя нужный сегмент спектра. Понятно, что указанная методика годится исключительно для видимого излучения и не затрагивает инфракрасный и ультрафиолетовый диапазоны.
Расчеты электрических цепей с помощью законов Кирхгофа.
Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.
Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E1=12 в и E2=5 в , с внутренним сопротивлением источников r1=r2=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.
Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:
I = I1 + I2,
так как I1 и I2 втекают в узел А, а ток I вытекает из него.
Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.
Для внешнего контура:
E1-E2 = Ur1 – Ur2 или E1-E2 = I1*r1 – I2*r2
Для внутреннего левого контура:
E1 = Ur1 + UR или E1 = I1*r1 + I*R
Итак, у нас получилась система их трех уравнений с тремя неизвестными:
I = I1 + I2;
E1-E2 = I1*r1 – I2*r2;
E1 = I1*r1 + I*R.
Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:
I = I1 + I2;
7 = 0,1I1 – 0,1I2;
12 = 0,1I1 +2I.
Далее из первого и второго уравнения выразим ток I2
I2=I — I1;
I2 = I1 – 70;
12 = 0,1I1 + 2I.
Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:
I — I1= I1 – 70;
12 = 0,1I1 + 2I.
Выражаем из первого уравнения значение I
I = 2I1– 70;
И подставляем его значение во второе уравнение
12 = 0,1I1 + 2(2I1 – 70).
Решаем полученное уравнение
12 = 0,1I1 + 4I1 – 140.
12 + 140= 4,1I1
I1=152/4,1
I1=37,073 (А)
Теперь в выражение I = 2I1– 70 подставим значение
I1=37,073 (А) и получим:
I = 2*37,073 – 70 = 4,146 А
Ну, а согласно первому закона Кирхгофа ток I2=I — I1
I2=4,146 — 37,073 = -32,927
Знак «минус» для тока I2 означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I2 вытекает из узла А.
Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.
Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Для закрепления результатата предлагаю посмотреть подготовленное мной видео:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Еще в этом выпуске журнала…
2. Практика. Как пользоваться мультиметром 3. Софт: Полезные советы по работе с программой для черчения электрических схем sPlan 7.
Алгебраическая сумма разностей потенциалов
Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:
ΣV = 0
Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.

Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути.
Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.
Одиночный контурный элемент — резистор
Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).
Будет интересно➡ Что такое статическое электричество и как от него избавиться
Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.
Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.
Закон Кирхгофа в химии
Когда в ходе химреакции система меняет свою теплоёмкость, вместе с тем меняется и температурный коэффициент возникающего в результате этого процесса теплового эффекта. Применяя уравнение, вытекающее из этого закона, можно рассчитывать тепловые эффекты в любом диапазоне температур. Дифференциальная форма этого уравнения имеет вид:
∆Cp = d∆Q/dT,
где:
- ∆Cp – температурный коэффициент;
- d∆Q – изменение теплового эффекта;
- dT – изменение температуры.
Важно! Коэффициент определяет, как изменится тепловой эффект при изменении температуры на 1 К (2730С).
Теорема Кирхгофа для термодинамики
Третье уравнения Максвелла, а также принцип сохранения зарядов позволили Густаву Кирхгофу создать два правила, которые применяются в электротехнике. Имея данные о значениях сопротивлений резисторов и ЭДС источников питания, можно рассчитывать протекающий I или приложенное U для любого элемента цепи.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

Рис. 4. Магнитные контуры цепей
В частности: ∑Ф=0.
Читайте также: Норматив потребления электроэнергии, что такое социальная норма потребления электроэнергии, средний расход электроэнергии в квартире за месяц на человека без счетчика
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Результат
Отлично!Попытайтесь снова(
Выбор направления токов
Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.
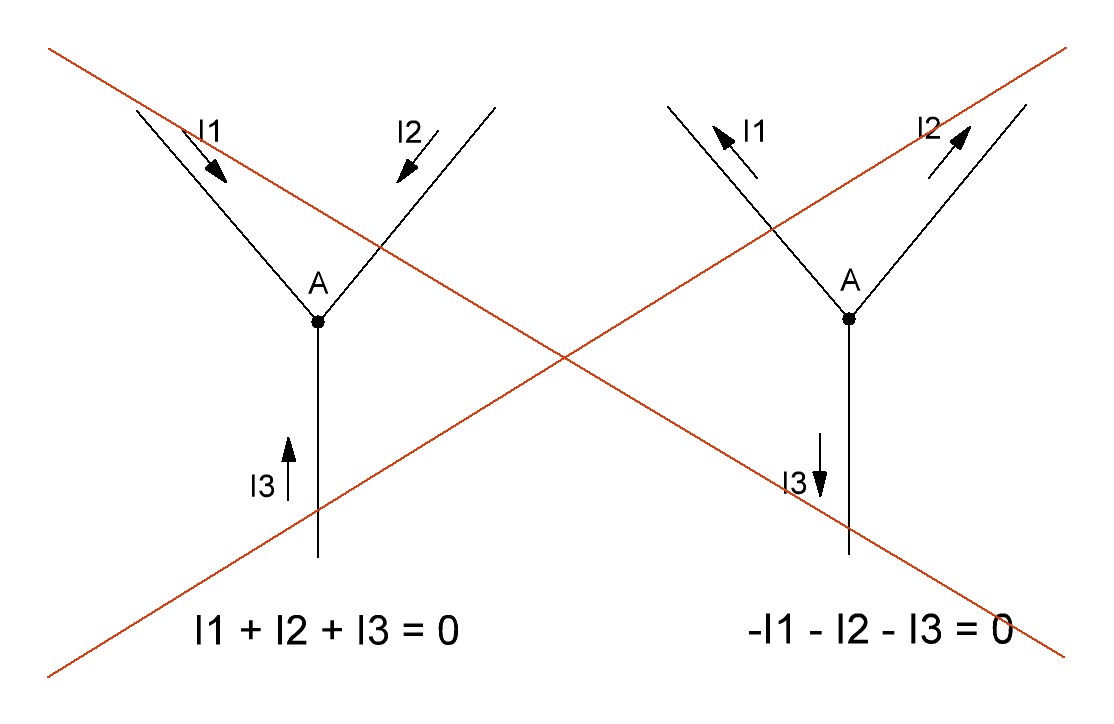
Например
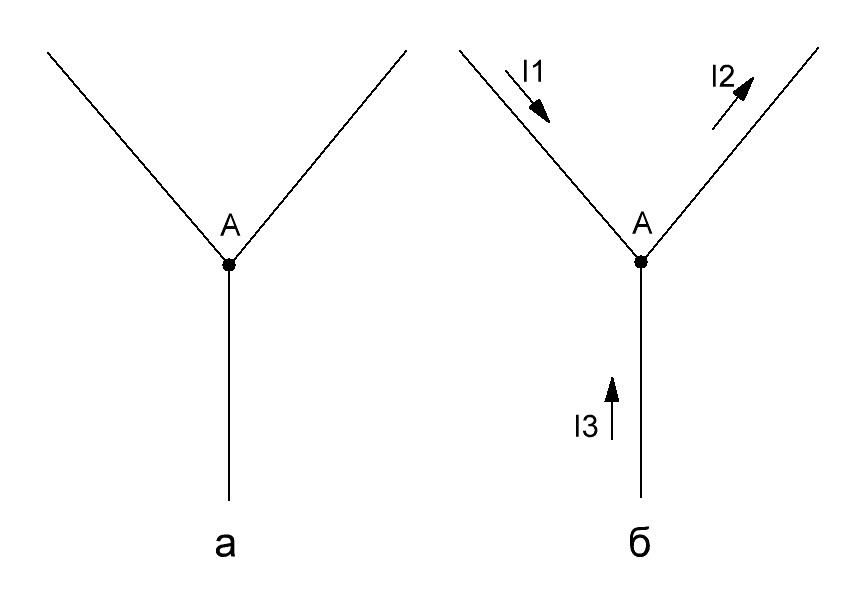
Рисунок 2
На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.
Предположим, что после расчёта цепи получились следующие значения токов:
I1 = -5 А;
I2 = -2 A;
I3 = 3 А.
Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).
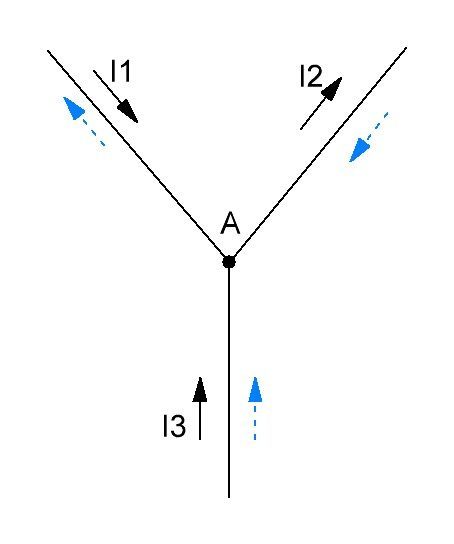
Рисунок 3 — действительное направление токов обозначено синими стрелками
- I1 − I2 + I3 = 0;
- -5 − (-2) +3 = 0;
- -I1 + I2 + I3 = 0;
- -5 + 2 +3 = 0.
Закон Кирхгофа для теплового излучения
Данный закон имеет другое название «третий закон». Сперва для лучшего понимания введем понятие теплового излучения. Принято называть тепловым излучение электромагнитное излучение, возникающее благодаря чужеродной энергии вращательного и колебательного движения атомов, молекул. Данное явление можно обнаружить абсолютно у всех тел, имеющих температуру не равняющуюся нулю или меньше. Основной количественной характеристикой теплового излучения выступает энергетическая светимость. Она должна быть вычислена одной из первых или же указана в условиях. Рассчитать её самостоятельно весьма проблематично. Её значение не постоянное, оно может меняться в зависимости от определенных характеристик: оказывает влияние температура окружающей среды, а также уровень нагретости тела. Имеет значение и длина, чем длиннее — тем значение меньше.
Читайте также: Проверка УЗО на срабатывание в домашних условиях
Формула выглядит таким образом:
R = E/(S·t), [Дж/(м2с)] = [Вт/м2]
Ещё одной характеристикой остаётся спектральная плотность энергетической светимости.
Важно ввести ещё одно понятие: коэффициент поглощения – это отношение поглощенной телом энергии к падающей энергии. Только теперь перейдем непосредственно к выделенному закону. Первое, что нужно сказать, что тепловое излучение является равновесной величиной. Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:
Закон для теплового излучения
Раннее указанная формула будет верной даже тогда, когда какое-либо тело из указанных будет АЧ:
Закон звучит данным образом: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.
Закон Кирхгофа для термодинамики
Кирхгоф показал, что соотношение излучательной и поглощательной способности твёрдого тела не зависит от вещества, но считается функцией частоты и температуры при термодинамическом равновесии. Особенно интересной абстракцией в этом плане стало абсолютно-чёрное тело. Это объект, поглощающий падающее на него излучение. Для него формула, представленная на рисунке упрощается. Излучающая способность абсолютно-чёрного тела описывает функцию формулы для прочих тел. Эта ипостась имеет максимум, определяемый законом смещения Вина и амплитуды, определяемую первым законом Вина (частным случаем считается формула Планка).
Отношение излучательной и поглощательной способности любого тела находится по формулам для любых температур и частот. При помощи спектрометра возможно оценить испускаемые волны. Это позволяют теоретически предсказать поглощательную способность любого предмета. На практике подобные исследования приводят к созданию объектов типа самолёт-невидимка, с трудом видимый локаторами.
Из закона сохранения энергии следует, что полное излучение равняется поглощению в термодинамическом равновесии. Значит, по всему спектру их соотношение равняется единице. До признания закона Кирхгофа уже установлено, что – чем лучше тело поглощает энергию, тем оно больше излучает. Обратите внимание, спектральные плотности поглощения и излучения имеют разную форму. В этом и заключается гениальное прозрение Кирхгофа. Взаимодействие определяется законом Вина и на графике выглядит подобно горе с вершиной, смещённой влево относительно центра фигуры.
Это позволяет понять, где находится максимум излучения (на макушке). Во всех участках графика, где линия находится ниже единицы, тело преимущественно поглощает энергию. Благодаря законам возможно предсказать температуру звёзд, к примеру, по цвету, а каждый кузнец знает, что деталь в горне дошла до кондиции лишь по характерному оттенку свечения. Это практические проявления законов Вина и Кирхгофа.
Вторым интересным наблюдением становится температура. Из графиков плотности излучения видно, чем показатель больше, тем активнее идёт излучение. В частности, звезды не поглощают энергию за малым исключением, но преимущественно излучают. У холодных планет преобладает противоположный процесс. Тело излучает, если его температура выше окружающей среды. В остальных ситуациях преобладает поглощение энергии.

Аналогия закона Кирхгофа
О значении для электротехники
RS триггер
Кирхгоф вывел правила, носящие абсолютный прикладной характер для решения практических вопросов в электротехнике. Комплексные применения вместе с иными методами дают возможность рассчитывать участки схем любой сложности. Эти два закона можно употребить для нахождения электрических параметров линейной алгебры.
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
Рис. 4. Иллюстрация второго правила Кирхгофа
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.