Чему равна электроемкость конденсатора? Конденсатор. Энергия электрического поля

Электроемкость

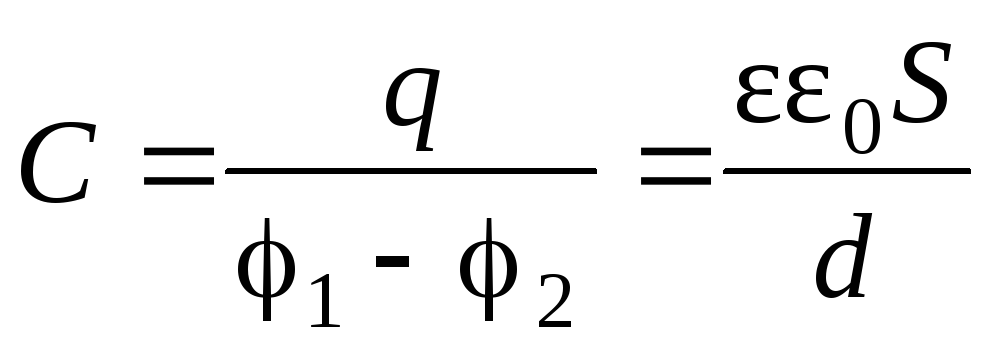
Электроемкость — это скалярная величина, характеризующая способность проводника накапливать электрический заряд.

Электроемкость:

не зависит от q и U;
зависит от геометрических размеров проводника, их формы, взаимного расположения, электрических свойств среды между проводниками.

Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу:

единица измерения емкости в СИ: Ф (фарад)

Конденсатор обладает свойством накапливать и сохранять электрическую энергию. Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.

Материал по теме: Как проверить конденсатор

Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками. Основные слагаемые электроемкости представлены на рисунке ниже:

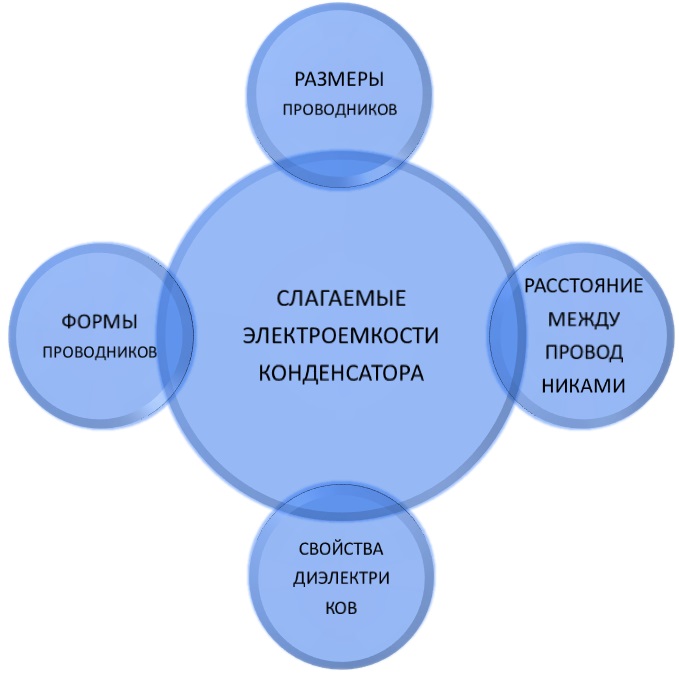
Основные слагаемые электроемкости.

Обозначение на электрических схемах:

Все электрическое поле сосредоточено внутри конденсатора.
Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.

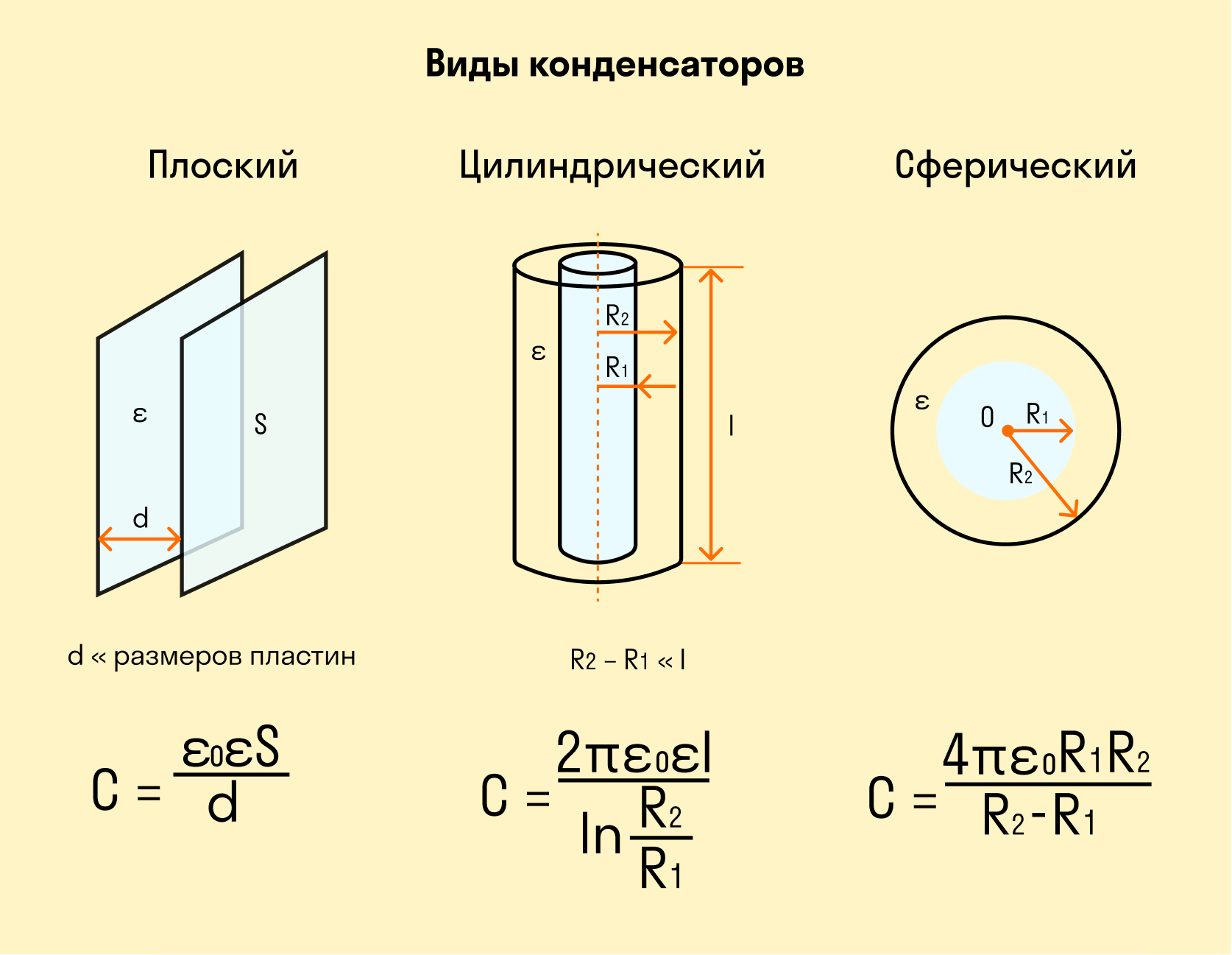
Виды конденсаторов:

по виду диэлектрика — воздушные, слюдяные, керамические, электролитические.
по форме обкладок — плоские, сферические.
по величине емкости — постоянные, переменные (подстроечные).

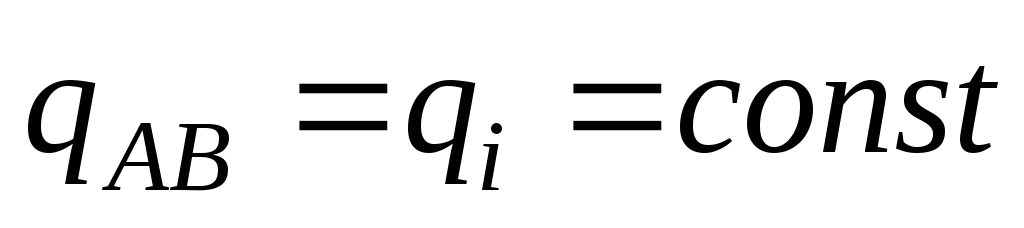
Электроемкость.

Электроемкость плоского конденсатора

где S — площадь пластины (обкладки) конденсатора

d — расстояние между пластинами
εо — электрическая постоянная

ε — диэлектрическая проницаемость диэлектрика

Конденсатор — это система заряженных тел обладает энергией.

Энергия любого конденсатора:

где С — емкость конденсатора, (Ф) W— энергия (Дж)
q — заряд конденсатора, (Кл)
U — напряжение на обкладках конденсатора, (В

Энергия равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или работе по разделению положительных и отрицательных зарядов необходимой при зарядке конденсатора. Конденсаторы применяются для накопления электрической энергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в радиотехнике: колебательный контур, выпрямитель и других радиоэлектронных устройствах.

Электрическая емкость конденсатора

Дальнейшие опыты с распределением электричества по поверхности наэлектризованного проводника, проводимые Кулоном и другими естествоиспытателями, позволили установить, что равномерное распределение электричества имеет место только на правильной шаровой поверхности. В общем случае заряд неравномерен и зависит от формы проводника, будучи больше в местах большей кривизны. Отношение количества электричества на части поверхности проводника к величине этой поверхности назвали плотностью (толщиной) электрического слоя. Экспериментально было установлено, что электрическая плотность и электрическая сила особенно велики в местах поверхности, имеющих наибольшую кривизну, особенно на остриях.

Интересный материал для ознакомления: что такое вариасторы.

Величину, характеризующую зависимость потенциала наэлектризованного проводника от его размеров, формы и окружающей среды, называют электроемкостью проводника и обозначают буквой С. Электроемкость проводника измеряется количеством электричества, необходимым для повышения потенциала этого проводника на единицу:

Будет интересно➡ Что такое статическое электричество и как от него избавиться

С = q/ϕ.

За единицу электроемкости в системе СИ принимается 1 фарада (1 Ф). Фарадой называется электроемкость проводника, которому для повышения его потенциала на один вольт нужно сообщить один кулон электричества. Электроемкостью, равной 1 Ф, обладал бы шар радиусом 9·10 6 км, что в 23 раза больше расстояния от Земли до Луны. Если проводник соединить с источником электричества определенного потенциала, то проводник получит электрический заряд, зависящий от емкости проводника. Его емкость, а, следовательно, и количество электричества, которым он заряжается, увеличиваются, если приблизить к нему второй проводник, соединенный с землей.

Конструкция, состоящая из двух проводников, разделенных изолятором, с электрическим полем между ними, все силовые линии которого начинаются на одном проводнике, а заканчиваются на другом, была названа электрическим конденсатором. При этом оба проводника называются обкладками, а изолирующая прокладка – диэлектриком. Процесс накопления зарядов на обкладках конденсатора называется его зарядкой. При зарядке на обеих обкладках накапливаются равные по величине и противоположные по знаку заряды.

Поскольку электрическое поле заряженного конденсатора сосредоточено в пространстве между его обкладками, то электроемкость конденсатора не зависит от окружающих тел. Электроемкость конденсатора измеряется отношением количества электричества на одной из обкладок к разности потенциалов между обкладками:

С = q/ U.

1 Ф – электроемкость такого конденсатора, который может быть заряжен количеством электричества, равным 1 Кл, до разности потенциалов между обкладками, равной 1 В. Например, электрическая емкость плоского конденсатора в системе СИ определяется по соотношению:

С =εε 0 S/ d, где ε – диэлектрическая проницаемость материала, находящегося между обкладками конденсатора; ε 0 – диэлектрическая проницаемость вакуума; S – величина площади поверхности пластины (меньшей, если они не равны); d – расстояние между пластинами.

Если обкладки заряженного конденсатора соединить проводником, то заряды будут переходить с одной обкладки на другую и нейтрализуют друг друга. Этот процесс называется разрядкой конденсатора. Каждый конденсатор рассчитан на определенное напряжение. Если напряжение между обкладками станет слишком большим, то разрядка может произойти и непосредственно через диэлектрик (без соединительного проводника), т.е. получится пробой диэлектрика.

Будет интересно➡ Что такое резонанс, в чем его польза и опасность

Пробитый конденсатор к дальнейшему употреблению не пригоден. Для получения электроемкости нужной величины конденсаторы соединяют в батарею. На практике встречается как параллельное, так и последовательное соединение конденсаторов.

Строение конденсатора.

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:

C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.

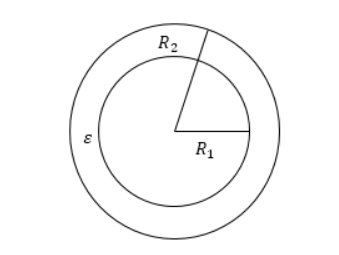
Рисунок2

Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание

История

Нетерпеливым читателям докладываем: Алессандро Вольта ввел собственно термин емкости. Неизвестно точно, употреблял ли кто раньше, но в своей работе итальянский ученый, называя электрофорус конденсатором, одновременно применяет к нему термин емкости. Как сосуду, куда можно «налить» заряд из емкости. Конденсатором зовет за схожесть процесса с осаждением паров: понемногу наберем произвольное количество электричества. По большому счету, это верно.

Термин конденсатор

Исторически первым конденсатором считают лейденскую банку. Поныне ходят споры, кто изобрел прибор, поскольку оба ученых, увлеченных событиями, избегали ведения аккуратных записей. Бесспорно одно – электроемкость прибора измерить было нельзя, отсутствовало соответствующее понятие «электроемкость конденсатора».

Скрин печатного варианта трактата Вольты, 1782 год

Придумавший термин бессилен произнести слово раньше, нежели Алессандро Вольта в 1782 году, докладывая Королевскому Научному обществу изыскания в области электростатики, чтобы понять, откуда берется электричество. Известно, в течение следующих пяти лет Луиджи Гальвани откроет «животное электричество», приведшее Вольту прямиком к созданию первого элемента питания. Докладывая обществу, молодой ученый лишен упомянутых знаний, светило пытается понять, откуда появляется заряд. Рассуждает приблизительно так: «К настоящему времени немало свидетельств существования атмосферного электричества. Люди бессильны найти следы присутствия. Вероятно, означает: созданные электроскопы слишком слабы, неспособны уловить столь тонкую материю. Следовательно, требуется найти способ забрать из воздуха флюиды».

Выполняя сказанное, Алессандро Вольта предлагает приспособление, называемое электрофорусом (не путать с электрофорной машиной). Прибор захватывает флюиды атмосферного проводника (воздуха). Принцип служения Вольте напоминает процесс конденсации: собирает электричество.

Электрофорус

Запад электрофорус называет генератором емкостного типа. Указанное выше позволяет полагать: подобное определение прилепилось благодаря написанному Английскому Королевскому обществу Вольтой. Устройство придумано другим человеком – шведским физиком Джоном Кларком Вилке. Случилось двумя десятилетиями ранее – 1762 год.

Ныне считается, популярность прибору придал Вольта, называя любимца вечным генератором электричества. Тоже по сути правильно, тереть резину можно тысячелетиями. Больше «конденсатор» напоминает (см. рис.) здоровенную печать. Сверху, помимо основной центральной ручки, стоит боковая – снятия отрицательного потенциала. Видим три слоя:

Подложка необязательна, на нее наклеивается резина.
Тонкий слой резины служит телом электризации трением.
Сверху – тонкий лист металла, снабженный двумя рукоятками, одна (центральная) изолирована.

Внешний вид электрофоруса

Начав работы, нужно убрать «печать», натереть резину шерстью. Затем гладкий диск ставится обратно. Площадь соприкосновения с резиной невелика из-за присутствующих шероховатостей, положительный заряд приобретается нескоро. Нужно выждать. Оператор на короткий миг заземляет крышку боковой ручкой, снимая отрицательный заряд, снизу остается положительный. Прикасаясь одной рукой к металлу, можно слышать хорошо различимый треск. Резина после поднятия крышки несет избыток электронов, позволяющий повторить опыт несколько раз (верится с трудом, некоторые источники говорят о сотне повторений).

Разнимая тела, резким движением потянув изолирующую рукоятку, оператор получает статическое электричество. Изобретение революционное, примечательно, появилось в считанные годы после отмены закона охоты на ведьм. По заявлению Вольты, круг резины делается по возможности тонким, в пределах 50-й доли дюйма. Удается получить наилучший результат. Лист металла фактически становится пластиной. В противном случае долго придётся ждать наполнения объема проводника. В простонародье «конденсатор» называют резиновым пирогом. Пирогом, покрытым металлической начинкой.

Действительно ли электрофорус является неисчерпаемым источником энергии? В идеальных условиях, хотя верится с трудом. Отрицательный заряд резины поляризует металлическую пластину, создавая некий потенциал. Вытесненные на внешнюю поверхность электроны снимаются прикосновением заземлителя. Остается разнять составные части электрофоруса. Уничтожив положительный заряд прикосновением, услышав звук проскочившей искры, можно заново начинать опыт.

Электрофорус действительно напоминает конденсатор. После снятия лишнего отрицательного заряда превращается фактически в упомянутый прибор. Долго храниться конденсатор не может, поскольку электроны с резины понемногу будут стекать на металл. Устройство разрядится. Фактически резина, металл отделены друг от друга воздухом, служащим диэлектриком. Вместо резины используем различные полимеры, например, Тефлон.

Осталось заметить: во времена Вольты не знали методов избавления резины от статического заряда. «Обкладка» конденсатора могла долгое время хранить груз электронов. Вольта предлагает для разрядки поместить образец под солнечные лучи, либо поводить рядом горящей свечой. Через ионизированное пламя электроны покидают конденсатор. Сегодня понятно, достаточно вымыть резину, чтобы следов не осталось статического напряжения. Для работы потребуется вновь высушить.

Подсказки к задачам

Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами:

Заряд системы после соединения:

q′=C1U1+C2U2

Электрическая емкость системы:

C′=C1+C2

Напряжение:

U′=q′C′..=C1U1+C2U2C1+C2..

Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

q′=C1U1−C2U2

Электрическая емкость системы:

C′=C1+C2

Напряжение:

U′=q′C′..=C1U1−C2U2C1+C2..

Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

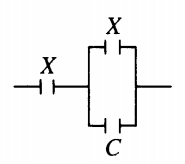
Электрическая емкость параллельного соединения равна:

Cпарал=X+C

Электроемкость последовательного соединения:

1Cпослед..=1Cпарал..+1X..=1X+C..+1X..

Учтем, что суммарная электроемкость равна C:

1C..=1X+C..+1X..

Преобразуем, умножим выражение на CX(X+C):

X(X+C)=CX+C(X+C)

Раскроем скобки:

X2+XC=CX+CX+C2

X2−CX−C2=0

Решив уравнение, получим: X = 25,9 пФ.

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C=2πεε0llnR2R1, где l — высота цилиндров, R1 и R2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.

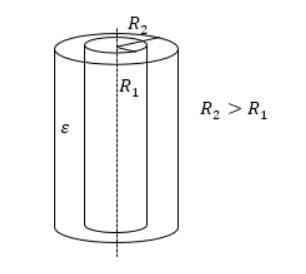
Рисунок3

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.

Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Как проверить емкость конденсатора

Если фабричные обозначения отсутствуют или повреждены, узнать номинал можно с помощью мультиметра в соответствующем режиме измерений.

На рисунке показан соответствующий диапазон положений переключателя типичного прибора

Проверять емкость можно по соотношению C =q/U с применением баллистического гальванометра. Этот специализированный прибор показывает заряд, проходящий через рабочую рамку. Аналогичное измерение не получится выполнить с применением серийного миллиамперметра, в котором привод стрелки обладает меньшей инерционностью. Для сравнения можно взять эталонный конденсатор с известной емкостью.

Проверка путём измерения времени зарядки

Вычислить емкость можно после преобразования рассмотренной выше формулы для таймера:

С = t/(In (1-U (t)/ (Uип — Uн) * R).

Для упрощенных расчетов надо запомнить, что за время t = C * 3R при подключении к источнику постоянного тока напряжение на выводах конденсатора увеличится до 95% от Uип. Соответственно, C = t/3R.

Измерение ёмкостного сопротивления

В частотно-зависимых цепях пригодится формула емкостного (Хс) сопротивления Xc = ½ * π * f *C, где f частота сигнала в цепи.

Проверка исправности тестером

Для уточнения исправности детали достаточно применить «прозвонку» или тестер. Токопроводящая цепь фиксируется в процессе заряда.

Заряд и разряд конденсаторов

Расчет емкости конденсатора

Рабочий цикл начинается после подключения в цепь источника тока. Перемещение электронов в батарею повышает положительный потенциал на обкладке. Аналогичный процесс увеличивает отрицательный заряд второго рабочего элемента. Рост напряженности поля ограничен напряжением АКБ (U). Накопленную энергию (W) можно определить следующим образом:

W = d *q2/(2*e0*S) = (U2 * C)/2.

Рабочие циклы

Чтобы зарядить конденсатор через резистор, понадобится определенное время:

t = In (1-U (t)/ (Uип — Uн) * R * C,

где:

U(t)/Uип/ Uн – напряжение изменения на конденсаторе/источника питания/ начального уровня, соответственно;
C – электроемкость плоского конденсатора;
R – электрическое сопротивление.

По этой формуле можно определить резистор, который надо установить в цепь для получения определенного временного интервала. Данная схема – пример простейшего функционального таймера. Для привода в действие исполнительного механизма к выходу можно подсоединить реле либо иной ключ с расчетом на необходимый уровень напряжения срабатывания. По аналогичной схеме происходит разрядка, показанная в нижней части рисунка.

Второй способ применения с пользой времени задержки – сглаживание пульсаций. Даже при сильном, но слишком коротком сигнале на входе напряжение на выходе не успеет измениться. Такое защитное устройство отличается простотой и надежностью при точном расчете компонентов схемы.

Виды конденсаторов

Допустимое напряжение

В предыдущих разделах показано, от чего зависит электроемкость конденсатора. Этот важнейший параметр корректируют с учетом необходимого класса точности. В сложных ситуациях применяют подстроечные модификации. Проверка тестером (осциллографом) поможет выполнить настройку схемы.

Однако для выбора подходящего компонента необходимо учитывать дополнительные характеристики:

при поддержании заданного уровня номинального напряжения конденсатор выполняет свои функции в течение длительного срока службы;
по удельной емкости определяют накопительные свойства в расчете на единицу объема;
некоторые модели (с электролитом, оксидным диэлектриком) подключают с учетом полярности выводов.

Обязательно следует обратить внимание на допустимое напряжение. Превышение этого порога провоцирует пробой. Некоторые диэлектрики способны восстанавливать функциональность. Другие – полностью выходят из строя после подобного воздействия.

Длительные рабочие циклы в предельных режимах, внешний перегрев или естественное старение способны повысить внутреннее давление до взрывоопасного уровня. Уменьшают вероятность сильных повреждений встроенным клапаном. Также применяют специальные насечки на торцевой части корпуса, которые формируют линии планового разрыва при возникновении аварийной ситуации.

Для повышения точности выбора пользуются дополнительной справочной информацией. Потери и ухудшение основных параметров определяют по следующим критериям:

электрическое и эквивалентное сопротивление изделия;
паразитная индуктивность;
самостоятельный разряд;
зависимость емкости от температуры;
остаточные явления поляризации.

К сведению. Если необходимые сведения в сопроводительных документах отсутствуют, узнать точные данные можно на официальном сайте производителя.

В следующем перечне приведены особенности распространенных видов конденсаторов:

масляные с бумажным диэлектриком рассчитаны на сравнительно низкий частотный диапазон;
энергонакопительные модели отличаются большими габаритами;
гигроскопичность бумажных слоев без наполнителя ограничивает область применения средой с низкими показателями относительной влажности;
диэлектрик из полиамида сохраняет работоспособность при высокой температуре (более +220°C), но значительно увеличивает себестоимость;
поликарбонат обеспечивает отличные диэлектрические параметры и влагостойкость, но применяют такие изделия при температуре не выше +120°C;
устойчивостью к внешним неблагоприятным воздействиям отличаются стеклянные и керамические конденсаторы.

Отдельно следует отметить новое направление – со слоем диэлектрика из ионов лития. По сравнению с аналогичными аккумуляторами, конденсаторы менее опасны, так как конструкция блокирует химические реакции с выделением газа при повышении температуры.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора $q$
, площадь обкладок $S$
.

Возьмём на второй обкладке настолько маленькую площадку, что заряд $q_0$
этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

$F_0 = q_0E_1,$

где $E_1$
— напряжённость поля первой обкладки:

$E_1=frac{displaystyle sigma }{displaystyle 2 varepsilon _0 vphantom{1^a}}=frac{displaystyle q}{displaystyle 2varepsilon_0 S vphantom{1^a}}.$

Следовательно,

$F_0=frac{displaystyle q_0q}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила $F$
притяжения второй обкладки к первой складывается из всех этих сил $F_0$
, с которыми притягиваются к первой обкладке всевозможные маленькие заряды $q_0$
второй обкладки. При этом суммировании постоянный множитель $q/(2 varepsilon_0 S)$
вынесется за скобку, а в скобке просуммируются все $q_0$
и дадут $q$
. В результате получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$
(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины $d_1$
до конечной величины $d_2$
. Сила притяжения пластин совершает при этом работу:

$A = F(d_1 - d_2).$

Знак правильный: если пластины сближаются $(d_2 < d_1)$
, то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины $A=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}left ( d_1-d_2 right )=frac{displaystyle q^2d_1}{displaystyle 2varepsilon_0 S vphantom{1^a}}-frac{displaystyle q^2d_2}{displaystyle 2varepsilon_0 S vphantom{1^a}}=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}}-frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}=W_1-W_2,$

где
$W_1=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}},$
$W_2=frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}$

Это можно переписать следующим образом:

$A = -(W_2 - W_1) = - Delta W,$

где

$W=frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}}.$
(12)

Работа потенциальной силы $F$
притяжения обкладок оказалась равна изменению со знаком минус величины $W$
. Это как раз и означает, что $W$
— потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение $q = CU$
, из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

$W=frac{displaystyle qU}{displaystyle 2 vphantom{1^a}},$
(13)

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}.$
(14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью $varepsilon$
. Сила притяжения обкладок уменьшится в $varepsilon$
раз, и вместо (11) получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 varepsilon S vphantom{1^a}}.$

При вычислении работы силы $F$
, как нетрудно видеть, величина $varepsilon$
войдёт в ёмкость $C$
, и формулы (12) — (14)останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Расчёт ёмкости плоских конденсаторов

Емкость конденсатора: формула

В идеальных условиях для определения емкости конденсатора (C0) можно применить формулу:

С0 = q/ U.

Диэлектрические свойства промежуточного слоя учитывают дополнением C = C0 * e.

Базовая единица (фарад или сокращенно Ф) слишком велика для типовых электротехнических схем. Поэтому применяют кратные уменьшительные приставки:

миллифарад (мФ) – 10-3 Ф;
микрофарад (мкФ) – 10-6 Ф;
нанофарад (нФ) – 10-9 Ф;
пикофарад (пФ) – 10-12 Ф.

Емкость один фарад соответствует накопленному единичному заряду (1 Кл), который создает разницу потенциалов на пластинах 1 В. По формуле емкости шара можно вычислить потенциал Земли –700 микрофарад.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Без него не будет работать ни один прибор. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Соединения конденсаторов

	Последовательное соединение	Параллельное соединение
Схема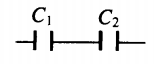
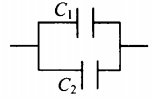Напряжение	U=U1+U2	U=U1=U2
Заряд	q=q1=q2	q=q1+q2
Электроемкость	1C..=1C1..+1C2..	C=C1+C2

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух $left ( varepsilon =1 right ).$

Пусть заряды обкладок равны $+q$
и $-q$
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина $q$
— заряд положительной обкладки — называется зарядом конденсатора.

Пусть $S$
— площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

$E_+ = E_-=frac{displaystyle sigma }{displaystyle 2 varepsilon_0 vphantom{1^a}}.$

Здесь $E_+$
— напряжённость поля положительной обкладки, $E_-$
— напряженность поля отрицательной обкладки, $sigma$
— поверхностная плотность зарядов на обкладке:

$sigma =frac{displaystyle q}{displaystyle S vphantom{1^a}}.$

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля $vec{E}$
имеем:

$vec{E} = vec{E}_+ + vec{E}_-$

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

$E = E_+ - E_-=0.$

Внутри конденсатора поле удваивается:

$E = E_+ + E_-= frac{displaystyle sigma }{displaystyle varepsilon_0},$

или

$E = frac{displaystyle q}{displaystyle varepsilon_0 S vphantom{1^a}}.$
(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно $d$
. Поскольку поле внутри конденсатора является однородным, разность потенциалов $U$
между обкладками равна произведению $E$
на $d$
(вспомните связь напряжения и напряжённости в однородном поле!):

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 S vphantom{1^a}}.$
(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

$C=frac{displaystyle q}{displaystyle U vphantom{1^a}}.$
(6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на $1$
В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

$C=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}}.$
(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью $varepsilon$
. Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в $varepsilon$
раз, так что вместо формулы (4) теперь имеем:

$E=frac{displaystyle q}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$
(8)

Соответственно, напряжение на конденсаторе:

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$
(9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

$C=frac{displaystyle varepsilon_0 varepsilon S}{displaystyle d vphantom{1^a}}.$
(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}} cdot frac{displaystyle (Ed)^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}Sd.$

Но $Sd = V$
— объём конденсатора. Получаем:

$W=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}V.$
(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля $E$
, сосредоточенного в некотором объёме $V$
.

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина $omega = W/V$
— энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

$omega =frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}.$
(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в $varepsilon$
раз, и вместо формул (15) и (16) будем иметь:

$W =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}V.$
(17)

$omega =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}.$
(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Поделиться страницей

От чего зависит электроемкость конденсатора

Энергия конденсатора

Определить этот параметр можно по формуле:

C = d * e0*e * S.

Здесь, кроме отмеченных выше величин, добавлено расстояние (d) между пластинами. Понятна прямая зависимость от размеров обкладок, расстояния между ними, диэлектрических свойств промежуточного слоя.

Это соотношение объясняет необходимость применения рулонных конструкций. Типовое решение – создание чередующихся слоев из металлического проводника (фольга 8-15 мкм) и бумаги (6-7 мкм).

онструкции керамических дисковых, трубчатых и литых конденсаторов

На рисунке отмечены следующие детали:

пластины;
внутренние электроды;
керамика (диэлектрик);
выводы.

Уменьшение расстояния между обкладками, кроме ухудшения накопительных свойств, повышает вероятность электрического пробоя.

Электроемкость конденсаторов

Электроемкость

Электрическая емкость конденсатора

Сферический конденсатор

История

Термин конденсатор

Электрофорус

Подсказки к задачам

Цилиндрический конденсатор

Как проверить емкость конденсатора

Проверка путём измерения времени зарядки

Измерение ёмкостного сопротивления

Проверка исправности тестером

Заряд и разряд конденсаторов

Виды конденсаторов

Допустимое напряжение

Энергия заряженного конденсатора

Расчёт ёмкости плоских конденсаторов

Применение конденсаторов

Пример раз — вспышка

Соединения конденсаторов

Ёмкость плоского конденсатора

Энергия электрического поля

От чего зависит электроемкость конденсатора

admin

Электроемкость

Электрическая емкость конденсатора

Сферический конденсатор

История

Термин конденсатор

Электрофорус

Подсказки к задачам

Цилиндрический конденсатор

Как проверить емкость конденсатора

Проверка путём измерения времени зарядки

Измерение ёмкостного сопротивления

Проверка исправности тестером

Заряд и разряд конденсаторов

Виды конденсаторов

Допустимое напряжение

Энергия заряженного конденсатора

Расчёт ёмкости плоских конденсаторов

Применение конденсаторов

Пример раз — вспышка

Соединения конденсаторов

Ёмкость плоского конденсатора

Энергия электрического поля

От чего зависит электроемкость конденсатора

Похожие записи:

admin

Связанные записи