Понятие сопротивление доходчиво

Электрическое сопротивление – это величина, которая определяет способность проводника пропускать электрический ток. Полезно также освежить знания про электрический ток

Представить это проще всего, исходя из строения металлов.

По классической теории металл состоит из кристаллической решетки, а между структурными элементами этой решетки путешествуют свободные электроны.

Внешнее электрическое поле заставляет их перемещаться и образуется электрический ток, т.е. направленное упорядоченное движение частиц.

Решетка металла мешает им двигаться по своему объему. Электроны трутся об её узлы и не могут протиснуться. Вот это явление и образует сопротивление. Это “сила”, которая мешает перемещению.

Ситуация аналогично ситечку на раковине. Вода проходит, но медленнее, чем проходила бы без ситечка.

Аналогичная ситуация присутствует во всех материалах, правда род и тип частичек может меняться. Тип строения тоже разный. Но условно можно принять, что всегда структура мешает им двигаться что в дереве, что в металле.

В некоторых телах вообще таких частичек не будет, там сопротивление бесконечное (некоторые виды резин, например).

Обратите внимание, что мы не рассматриваем тут понятие электрического тока и напряжения, т.к. это отдельные темы и если есть непонимание, обязательно напишите об этом в комментариях. Правда про электрический ток есть наше видео . Эти вещи нужно четко понимать.

Ну и из сказанного очевидно, что сопротивление будет зависеть от геометрических параметров проводника (т.е. площадь сечения S, длина l) и типа проводника (который тут описывается понятием удельное сопротивление и является табличной величиной). Ещё оно зависит от температуры (чем выше тем больше для большинства тел), но это мы совсем от самого закона уходим… Для задачек на закон Ома знаний уже вполне достаточно.

Формулировка закона Ома

В результате множества экспериментов Ом вывел зависимость, которая определяет связь между силой тока в проводнике, напряжением и тем самым сопротивлением, которое мы описали выше.

Звучит закон так: Cила тока на участке электрической цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению

Вроде как все слова тут понятные, если знать все определения. Сопротивление мы разобрали. Сила тока – это, грубо говоря, количество частичек, которое окажется в проводнике. Понятие сила тока подробно я разбирал в этой статье , обязательно прочитайте её.

Напряжение – это “поток”, который эти частицы несет. Вот вроде бы всё и увязали.

Если рассматривать цепь, то сопротивление по элементам распределяется согласно их техническим характеристикам и вычисляется согласно закону Ома. Т.е. мы не можем утверждать, что на каждом элементе есть одинаковое сопротивление.

Например, если в цепи с последовательным подключением две лампочки, т омы помним что сила тока во всей цепи при таком соединении одинаковая, а вот напряжение на элементах разное. Замеряем его на точках подключения лампочек, записываем и запихиваем в закон Ома. Вот всё и посчитали :)…

Закон Ома для участка цепи

Когда закон ома записан в такой форме, как мы привели выше, то он называется закон ома для участка цепи.

Читайте также  Электропроводка в доме своими руками – пошаговая схема разводки и монтажа электрики

Почему для участка цепи? Для участка, потому что тут не учитывается сопротивление всей цепи. Можно измерить сопротивление на каждом участке исходя из приведенных характеристик.

Закон Ома для полной цепи

Полной цепью (в отличие от участка цепи, применительно к которому мы излагали всё выше) называется цепь с учетом источника тока.

Почему это важно?

Именно потому, что если мы представим себе электрическую цепь условно как систему труб для воды, то участок цепи это будет незамкнутый кусок трубы, а полная цепь – зацикленная система.

Из примера может показаться, что участок цепи есть незамкнутая в электрическом смысле цепь. Нет, пример приведен не для этого. И там, и там электрическая цепь замкнута.

Просто нам нужно обозначить, что без учета источника тока и его внутреннего сопротивления (r) цепь не полная, а расчёт не всегда способен учитывать все значимые характеристики.

Ну а внутреннее сопротивление, как вы наверное догадались – это то сопротивление, которым обладает источник тока. Да, току в цепи сложно проходить и через сам источник! Даже сам источник провоцирует энергетические потери. А вот считать его аналогично расчёту для участка цепи нельзя.

Получается, что в закон Ома добавится ещё и внутренне сопротивление. И всё! Ничего страшного.

Формулировка закона Ома для полной цепи немного изменится. Теперь у нас слово напряжение заменится словом ЭДС (электродвижущая сила), а слово сопротивление заменится суммой внешнего сопротивления цепи и внутреннего сопротивления источника тока. Ну и формула будет такая:

Добавилось понятие электродвижущая сила (ЭДС), обозначенная в формуле E прописное. Что это за зверь?

ЭДС – это, по сути дела, и есть напряжение.

Разница в том, что если мы опять сравним напряжение с напором воды в водопроводе, то напряжением будет являться разница напора между двумя произвольными точками в водопроводе, а ЭДС – это напор на насосе, который качает воду.

При использовании термина ЭДС мы вспоминаем, что у источника есть внутреннее сопротивление, как оно есть и у насоса, который препятствует движению воды через самого себя. Если же мы считали бы именно напряжение источника, то мы бы приняли, что система идеальная и источник движению тока сам не препятствует.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Читайте также  Хлопковый выключатель: принцип работы, схема подключение и монтаж

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Следствия закона Ома.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Закон для переменного тока

Классический закон был открыт физиком из Германии Симоном Омом в 1862 году. Проводя эксперименты, он обнаружил связь между током и напряжением. В результате ученый сформулировал утверждение, что сила тока пропорциональна разности потенциалов и обратно пропорциональна сопротивлению. Если в электрической цепи ток уменьшится в несколько раз, то и напряжение в ней станет меньше на столько же.

Математически закон Ома был описан как:

I = U / R, А.

Это выражение справедливо как для синусоидального, так и для постоянного тока. Но такая зависимость величин соответствует идеальной ситуации, в которой не учитываются паразитные составляющие и сопротивление источника тока. В случае же гармоничного сигнала на его прохождение влияет частота, из-за присутствия ёмкостной и индуктивной составляющей в электрической линии.

Поэтому закон Ома для переменного тока описывается формулой:

Читайте также:  Правила безопасности при работе с электрическим инструментом

I = U / Z, где:

• I — сила переменного тока, А;
• U — разность потенциалов, В;
• Z — полное сопротивление цепи, Ом.

Полное сопротивление зависит от частоты гармоничного сигнала и вычисляется по следующей формуле:

Z = ((R+r)2 + (w*L — 1/w*C)2)½ = ((R+r)2+X2)½.

В то же время для переменного сигнала необходимо учитывать амплитудную и частотную составляющую. Поэтому:

P = I *U*cosw*t*cos (w*t+ Ψ), где I, U — амплитудные значения, а Ψ — фазовый сдвиг.

Для анализа процессов в электрических цепях переменного тока вводится понятие комплексного числа. Связанно это со смещением фаз, появляющихся между током, и разностью потенциалов. Обозначается это число латинской буквой j и состоит из мнимой Im и вещественной Re частей.

Так как на активном сопротивлении происходит трансформирование мощности в тепло, а на реактивном она преобразуется в энергию электромагнитного поля, возможны её переходы из любой формы в любую. Можно записать: Z = U / I = z * ej*Ψ.

Отсюда полное сопротивление цепи: Z = r + j * X, где r и x — соответственно активное и реактивное сопротивление. Если же сдвиг фаз принимается равный 90, то комплексное число можно не учитывать.

Закон Ома в интегральной форме для неоднородного участка цепи

Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:

интегральный закон Ома для участка цепи

где:

• 
  
  – сопротивление участка,
• 
  
  – работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,
• 
  
  – работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),
• 
  
  – абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).

Мнемоническая диаграмма для закона Ома

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

U — электрическое напряжение;
I — сила тока;
P — электрическая мощность;
R — электрическое сопротивление

В соответствии с этой диаграммой формально может быть записано выражение:

R=UI,(7){displaystyle R!={U over I},qquad (7)}

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

Читайте также  Какие общие требования предъявляются к электромонтажным инструментам

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

R=ϱls,(8){displaystyle R!={varrho l over s},qquad (8)}

где:

• ϱ{displaystyle varrho }
  
   — удельное электрическое сопротивление материала, из которого сделан проводник,
• l{displaystyle l}
  
   — его длина
• s{displaystyle s}
  
   — площадь его поперечного сечения

Принятые единицы измерения

Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:

• напряжение – в вольтах;
• ток в амперах
• сопротивление в омах.

Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.

Закон Ома для полной цепи

Определение: Сила тока в цепипропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

Формула I=frac{varepsilon}{R+r}

• varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

Отображение в дифференциальной форме

На подсчёт сопротивления влияет тип материи, по которой протекает электроток, а также геометрические габариты проводника.

Дифференциальная форма формулировки Ома, записывающаяся достаточно кратко, отображает электропроводящие характеристики изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.

Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:

Интересно!

Если исходить из научных данных, следует сделать вывод о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.

При использовании анизотропеновых электроэлементов нередко встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.

Отдельный участок и полная электрическая цепь

Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:

• Отдельный краткий участок. Является частью схемы без источника ЭДС.
• Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.

Другие формы закона Ома

Закон Ома в дифференциальной форме является крайне важным понятием для электротехники/электроники, поскольку он описывает как напряжение тока, так и сопротивление. Все это взаимосвязано на макроскопическом уровне. Изучая электрические свойства на макро- или микроскопическом уровне, используется более связанное уравнение, которое можно назвать «уравнением Ома», имеющее переменные, которые тесно связаны со скалярными переменными V, I и R закона Ома, но которые являются постоянной функцией положения в проводнике.

Переменный ток

Величины являются комплексными, если речь идёт о синусоидальных формах энерготока с циклической частотой, в цепях которых присутствуют активная ёмкость с индуктивностью.

В перечень комплексных величин входят:

• разность между потенциалами;
• сила тока;
• комплексное электросопротивление;
• модуль импеданса;
• разность индуктивного и ёмкостного сопротивлений;
• омическое электросопротивление;
• фаза импеданса.

Если несинусоидальный энерготок допустимо измерить временными показателями, закон ома для неполной электрической цепи может быть представлен в виде сложенных синусоидальных Фурье-компонентов. В линейной цепи составные элементы фурье-разложения являются независимо функционирующими. В нелинейных цепях образуются гармоники и множество колебаний. Таким образом, можно сделать вывод о невозможности выполнения правила Ома для нелинейной электроцепи.

Внимание!

Гармоника – это колебание, частота которого кратна частоте напряжения.

Движение тока по неоднородным проводникам

Закон Ома для неоднородного участка

Разность потенциалов, вызванная ЭДС, будет производить напряжение на клеммах генератора. ЭДС – это скалярная величина. При подключении к клеммам проводника через него потечёт ток, плотность которого выражается, например, Ī. Это уже векторная величина. Если ток создан только разностью потенциалов на клеммах, то векторы потенциала и плотности тока будут совпадать. Такой проводник называют однородным. Закон Ома для однородного участка цепи:

I=U/R.

Вектор напряжённости

Неоднородный проводник, кроме сил, которые образованы разностями потенциалов, имеет сторонние силы. Для определения плотности тока Ī пользуются законом Ома в дифференциальной форме для неоднородных проводников:

Ī=γ(E+Ē₁+ Ē₂+ Ēn).

Векторы и каждый участок проводника складываются, E – напряжённость, созданная разностью потенциалов на клеммах проводника (скалярная величина). Ē₁, Ē₂, Ēn – векторные величины напряжённости первой, второй и энной сторонних сил.

Так как γ – удельная проводимость проводника, обратная сопротивлению, ϕ₁ – потенциал на 1-ой точке, ϕ₂ – потенциал на 2-ой точке, то закон Ома для неоднородного участка цепи от 1-ой до 2-ой точки будет записываться так:

Ī =(ϕ₁ – ϕ₂+ Ē)/R.

Для ознакомления металлы и их удельное сопротивление:

• Серебро – 1,6×10ˉ⁸Ом×м;
• Медь – 1,72×10ˉ⁸ Ом×м;
• Алюминий – 2,6×10ˉ⁸ Ом×м;
• Латунь – 3…7,0×10ˉ⁸ Ом×м;
• Бронза – 8,0×10ˉ⁸ Ом×м;
• Железо – 9,8×10ˉ⁸ Ом×м;
• Свинец – 2.0×10ˉ⁶Ом×м;
• Графит – 3…5,0×10ˉ⁵Ом×м.

Как трактуется правило Ома

Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в условиях приближения незначительной частоты, плотности тока и напряжения электрополя. Следует отметить, что в ряде случаев как первый закон, так и второй закон, применяемый для полной цепи, не соблюдаются.

Существует теория Друде, для выражения которой используются следующие величины:

• удельная электропроводимость;
• концентрированное размещение электронов;
• показатель элементарного заряда;
• время затихания по импульсам;
• эффективная масса электрона.

Внимание!

Все формулы Ома – первый, второй физический закон ома и третий распространяются на омические компоненты.

Перечень условий, при которых становится невозможным соблюдения правила Ома:

1. высокие частоты с чрезмерно большой скоростью изменения электротока;
2. пониженная температура сверхпроводимого вещества;
3. перегрев проводника проходящим электротоком;
4. в ситуации пробоя, возникшего в результате подсоединения к проводниковому элементу высокого напряжения;
5. в вакуумной или газонаполненной электролампе;
6. для гетерогенного полупроводникового прибора;
7. при образовании пространственного диэлектрического заряда в контакте металлического диэлектрика.

Применение на линии электропередач

В процессе доставки на линию электропередач потери энергии должны быть минимизированы. Причиной энергетических потерь является нагрев провода, во время которого энергия электротока превращается в теплоэнергию.

Чтобы дать определение по закону ома потерянной мощности, необходимо показатель электрической мощности во второй степени умножить на внутреннее сопротивление источника напряжения и разделить на ЭДС в квадрате.

Из этого следует, что рост потери энергомощности осуществляется пропорционально протяжённости линии электропередач и квадрату электродвижущей силы.

Поскольку электродвижущую силу ограничивает прочность обмотки генератора, то повышение энергонапряжения возможно после того, как из генератора выйдет электроток, на участке входа линии.

Переменный ток легче всего распределяется по линии через трансформатор. Однако, поскольку следствием повышения энергонапряжения является потеря коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой линии электропередач не превышает миллиона вольт.

Внимание!

Поведение линии электропередач в пространстве подобно антенне, ввиду чего берётся во внимание потеря на излучение.

Неоднородный участок цепи постоянного тока

Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.

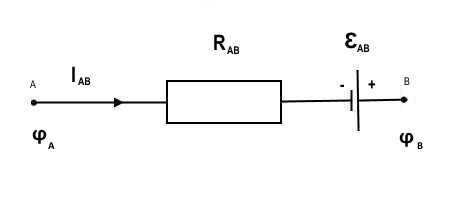
Схема неоднородного участка

Формула для такого участка (обобщенный закон) будет иметь следующий вид:

Формула для неоднородного участка цепи

9.Сопротивление и проводимость.

Сопротивление зависит от геометрии и от вещества, из которого сделан проводник.

Для цилиндрического проводника одинакового поперечного сечения оно вычисляется особенно просто.

Измерив сопротивление, можно вычислить ёмкость и наоборот.

Данное устройство иногда называется конденсатором с утечкой.

По физическому смыслу, удельное сопротивление – это сопротивление куба вещества с ребром 1 м, если подводящие провода подключены к центрам противоположных граней.

Приведем таблицу удельных сопротивлений

Медь	1,72·10-8Ом·м
Серебро	1,6·10-8Ом·м
Алюминий	2,6·10-8Ом·м
Свинец	2,0·10-6Ом·м
Графит	3·10-5Ом·м
Германий	0,6Ом·м
Стекло	10+9Ом·м

Закон Ома — основа электротехники

Это основное уравнение, используемое для изучения электрических цепей, было получено экспериментальным путем Георгом Симоном Омом. Он родился в Эрлангене Германии в 1787 году и поступил в университет этого города в 1805 году, где он получил докторскую степень. Георг преподавал математику в школах и проводил эксперименты по физике в школьной физической лаборатории, пытаясь понять принципы электромагнетизма.

Г. С. Ом

В 1827 году он опубликовал статьи, в которых описана математическая модель того, как контуры проводят тепло в работах Фурье. Ом получил экспериментальные данные, на базе которых впервые смог сформулировать свой закон 8 января 1826 года. Он установил, что разность потенциалов между двумя точками в цепи равна произведению тока между ними на общее сопротивление всех электрических устройств. Чем больше напряжение батареи или ее общая разность электропотенциалов, тем больше будет ее ток. Аналогично, с большим сопротивлением он будет меньше.

Но его исследования не нашли должного понимания и Георг оставил свою работу в Кельне. Только в 1833 году он получил должность профессора в Нюрнберге. Выводы Ома послужили катализатором для новейших исследований по электричеству. В 1841 году ученого наградили медалью Копли, а в 1872 году «Ом» был принят в качестве единицы сопротивления в электрических цепях.

Закон Ома для полной электрической цепи описывает протекание тока через проводящие металлы, когда применяются различные уровни напряжения. Некоторые материалы, такие как электропровода, имеют небольшое сопротивление току — этот тип материала называется проводником.

Важно! В других случаях материал может препятствовать протеканию тока, но, тем не менее, допускает его использование. В электрических цепях эти компоненты часто называют резисторами. Существуют материалы, которые практически не пропускают ток, они называются изоляторами.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

План:

1.Понятие о токе.

2.Плотность тока и сила тока.

3.Единицы силы и плотности тока.

4.Действия электрического тока.

5.Уравнение непрерывности.

6.Поле в проводнике при постоянном токе.

7.Закон Ома в дифференциальной форме.

8.Закон Ома в интегральной форме.

9.Сопротивление и проводимость.

10.Зависимость сопротивления от температуры.

11.Закон Джоуля – Ленца.

Важность закона Ома

Закон Ома в дифференциальной и интегральной форме, вероятно, являлся самым важным из ранних описаний физики электричества. Сегодня же мы считаем это почти очевидным, но, когда Ом впервые опубликовал свои работы, это было не так. Критики отнеслись к его трактовке с враждебностью. Они называли его работы «голыми фантазиями», а немецкий министр образования заявил, что «профессор, который проповедует такую ересь, недостоин преподавать науку».

Преобладающая в то время в Германии научная философия утверждала, что нет необходимости проводить эксперименты, чтобы развить понимание природы. Кроме того, брат Геогра, Мартин, математик по профессии, боролся с немецкой образовательной системой. Эти факторы препятствовали принятию работы Ома, и его работа не получила широкого признания до 1840-х годов. Тем не менее Ом получил признание за его вклад в науку задолго до его смерти.

Закон Ома в дифференциальной и интегральной форме представляет собой эмпирический закон, обобщение результатов многих экспериментов, которые показали, что ток примерно пропорционален напряжению электрического поля для большинства материалов. Он является менее фундаментальным, чем уравнения Максвелла, и подходит не во всех ситуациях. Любой материал будет разрушаться под силой достаточного электрического поля.

Закон Ома был соблюден на широком диапазоне шкал. В начале 20-го века закон Ома не рассматривался в атомном масштабе, однако эксперименты подтверждают обратное.

Переход от интегральной формы закона Ома к дифференциальной

Найдем связь между вектором плотности тока ($overrightarrow{j}$) и вектором напряженности электрического поля ($overrightarrow{E}$) в одной и той же точке проводящей среды. Если вещество изотропно, то $overrightarrow{j}uparrow uparrow overrightarrow{E}$. Выделим в окрестности рассматриваемой точки гипотетический цилиндр, образующие которого параллельны векторам напряженности поля и плотности тока (рис.1).

Готовые работы на аналогичную тему

• Курсовая работа Дифференциальная форма закона Ома 440 руб.
• Реферат Дифференциальная форма закона Ома 280 руб.
• Контрольная работа Дифференциальная форма закона Ома 200 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Рис. 1

Читайте также:  Что такое автоматическая частотная разгрузка и для чего она нужна

Через поперечное сечение цилиндра (dS) (рис.1) течет ток, сила которого запишется как:

Напряжение, приложенное к цилиндру можно выразить как:

где $E$ — напряжённость поля в рассматриваемой точке. Сопротивление цилиндра получит выражение:

Подставим формулы (3),(4),(5) в выражение (1), получим:

Проведем сокращения, получим:

Заменим удельное сопротивление ($rho $), на удельную проводимость ($sigma $). Используем то, что векторы напряженности и плотности тока имеют одинаковые направления окончательно запишем:

Уравнение (8) называется законом Ома в дифференциальной форме. В отличие от закона Ома в интегральной форме (1) уравнение (8) содержит величины, которые характеризуют электрическое состояние среды в точке.

Появились вопросы по этой теме? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос

Напряженность поля, которая входит в уравнение (8) — это поле внутри проводящей среды при наличии тока. Однако, если среда однородна, то в большинстве случаев это поле совпадает с электростатическим полем, то есть полем, которое было бы между электродами с таким же напряжением на них что и при наличии тока. Следовательно, в однородном проводнике линии напряженности электростатического поля совпадают с линиями тока.

Квантовое начало

Зависимость плотности тока от приложенного электрического поля имеет принципиально квантово-механический характер (классическая квантовая проходимость). Качественное описание закона Ома может быть основано на классической механике с помощью модели Друде, разработанной немецким физиком Паулем Друде в 1900 году. Из-за этого закон Ома имеет множество форм, например, так называемый закон Ома в дифференциальной форме.

Интерпретация

Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. К примеру, при двойном увеличении приложенного напряжения, интенсивность постоянного тока также удваивается.

Интересно!

Наиболее часто правило Ома применяется для металла и керамики.

История

В январе 1781 Генри Кавендиш экспериментировал с лейденской банкой и стеклянной трубой различного диаметра, наполненной раствором соли. Кавендиш писал, что скорость изменяется непосредственно как степень электрификации. Изначально результаты были неизвестны научному сообществу. Но Максвелл опубликовал их в 1879 году.

Ом сделал свою работу на сопротивлении в 1825 и 1826 годах и опубликовал свои результаты в 1827 году в книге “Гальваническая цепь доказана математически”. Вдохновлялся он работой французского математика Фурье, которая описывала теплопроводность. Для экспериментов он изначально использовал гальванические сваи, но позже перешел к термопарам, что смогло обеспечить более стабилизированный источник напряжения тока. Оперировался он понятиями внутреннего сопротивления и постоянного напряжения тока.

Также в этих опытах использовался гальванометр для измерения тока, так как напряжение между клеммами термопары пропорционально температуре соединения. Затем он добавил тестовые провода различной длины, диаметра и материала для завершения схемы. Он обнаружил, что его данные могут быть смоделированы с помощью следующего уравнения

x= a/b + l,

где x – показания измерительного прибора, l – длина испытательного проводника, a -зависящая от температуры соединения термопары, b – константа (постоянная) всего уравнения. Ом доказал свой закон на основе этих вычислений пропорциональности и опубликовал свои результаты.

5.Уравнение непрерывности

Закон сохранения заряда утверждает, что в замкнутой системе заряд сохраняется. Если система не замкнута, то заряд может изменяться.

Данное уравнение называется уравнением непрерывности в интегральной форме. Производная по времени связана с временной зависимостью заряда. Данное уравнение считается постулатом. По смыслу – это закон изменения заряда.

Используя понятие объемной плотности заряда и формулу Остроградского-Гаусса

получаем

– уравнение непрерывности в дифференциальной форме.

Если ток постоянный, то , следовательно, линии плотности тока являются замкнутыми.

2.Плотность тока и сила тока

Для характеристики постоянного тока вводят две физические величины: векторную – плотность тока и скалярную – сила тока.

Определение: Плотностью тока называется физическая величина, определяющая заряд, прошедший через площадку dS за время dt следующим образом.

Пусть все частицы одинаковые и имеют заряд q и скорость υ

, которая называется средней или упорядоченной или дрейфовой скоростью.

Определение: Силой тока называется поток плотности тока через какую-либо поверхность.

Силу тока можно определять как заряд, прошедший через поперечное сечение проводника за время Δt

. Данное выражение используется для определения единицы заряда.

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

J=n⋅e02⋅τm⋅E=σ⋅E.{displaystyle mathbf {J} ={frac {ncdot e_{0}^{2}cdot tau }{m}}cdot mathbf {E} =sigma cdot mathbf {E} .}

Здесь:

• σ{displaystyle sigma }
  
   — электрическая удельная проводимость;
• n{displaystyle n}
  
   — концентрация электронов;
• e0{displaystyle e_{0}}
  
   — элементарный заряд;
• τ{displaystyle tau }
  
   — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
• m{displaystyle m}
  
   — эффективная масса электрона.

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
• В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике) [4] .

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Интересно почитать: инструкция как прозвонить транзистор.