Калькулятор силы тока при параллельном соединении
Расчет силы тока по мощности, напряжению, сопротивлению
Бесплатный калькулятор расчета силы тока по мощности и напряжению/сопротивлению – рассчитайте силу тока в однофазной или трехфазной сети в ОДИН КЛИК!
Если вы хотите узнать как рассчитать силу тока в цепи по мощности, напряжению или сопротивлению, то предлагаем воспользоваться данным онлайн-калькулятором. Программа выполняет расчет для сетей постоянного и переменного тока (однофазные 220 В, трехфазные 380 В) по закону Ома. Рекомендуем без необходимости не изменять значение коэффициента мощности (cos φ) и оставлять равным 0.95. Знание величины силы тока позволяет подобрать оптимальный материал и диаметр кабеля, установить надежные предохранители и автоматические выключатели, которые способны защитить квартиру от возможных перегрузок. Нажмите на кнопку, чтобы получить результат.
Смежные нормативные документы:
- СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
- СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
- СП 76.13330.2016 «Электротехнические устройства»
- ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
- ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
- ГОСТ Р 50571.1-93 «Электроустановки зданий»
Правила работы на калькуляторе
В быту нас интересуют, как правило, четыре взаимосвязанных характеристики электричества:
- напряжение;
- ток;
- сопротивление;
- или мощность.
Если тебе известны две величины, входящие в закон Ома (U, R, I), то вводи их в соответствующие строки, а оставшийся параметр и мощность будут вычислены автоматически.
Будь внимательным, чтобы не допустить ошибки.
Читайте также: Как работают устройства автоматики повторного включения (АПВ) в электрических сетях
Все значения надо заполнять в одной размерности: амперы, вольты, омы, ватты без использования обозначений дольности или кратности.
Осуществить переход к ним тебе поможет наглядная таблица.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Формулы расчета силы тока
Электрический ток — это направленное упорядоченное движение заряженных частиц. Сила тока (I) — это, количество тока, прошедшего за единицу времени сквозь поперечное сечение проводника. Международная единица измерения — Ампер (А / A).
Читайте также: Выбор li-ion аккумулятора 18650 для шуруповерта
— Сила тока через мощность и напряжение (постоянный ток): I = P / U — Сила тока через мощность и напряжение (переменный ток однофазный): I = P / (U × cosφ) — Сила тока через мощность и напряжение (переменный ток трехфазный): I = P / (U × cosφ × √3) — Сила тока через мощность и сопротивление: I = √(P / R) — Сила тока через напряжение и сопротивление: I = U / R
- P – мощность, Вт;
- U – напряжение, В;
- R – сопротивление, Ом;
- cos φ – коэффициент мощности.
Коэффициент мощности cos φ – относительная скалярная величина, которая характеризует насколько эффективно расходуется электрическая энергия. У бытовых приборов данный коэффициент практически всегда находится в диапазоне от 0.90 до 1.00.
Источник
Последовательное включение
Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников. Расчёт общего значения импеданса в этом случае совсем несложен, для этого просто суммируются все номинальные значения элементов входящих в состав цепочки: Rобщ=R1+R2+…+Rn.
Например, в схеме применяется цепочка сопротивлений, состоящая из пяти резисторов: R1=32 Ом, R2=16 Ом, R3=1 кОм, R4=4,7 кОм, R5=1 Ом. После приведения всех номиналов к международной системе, получится ответ, равный: Rобщ = 32+16+1000+4700+10=5758 Ом или 5,75 кОм, что соответствует стандартному значению 5,6 кОм.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Калькулятор расчета параллельного соединения резисторов
Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов
Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.
Для этого вам необходимо:
- Указать в графе «количество резисторов» их число, в нашем примере их три;
- После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
- Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.
Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.
Для расчета суммарного сопротивления калькулятором используется такое соотношение:
- Rсум — суммарное сопротивление параллельно соединенных элементов
- R1 — сопротивление первого резистора;
- R2 — сопротивление второго резистора;
- R3 — сопротивление третьего резистора;
- Rn — сопротивление n-ого элемента.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Цветовая маркировка резисторов с пятью и шестью полосками онлайн расчет
Калькулятор резисторов с пятью цветными полосками:
Для определения сопротивления у резисторов с шестью полосами нужно использовать калькулятор элементов с пятью полосками и учесть шестую цветную полосу, которая означает температурный коэффициент сопротивления. Подробная таблица значений температурного коэффициента сопротивления (ТКС) и их привязка к конкретному цвету приведена в следующей таблице:
| Цвет | ТКС (ppm/ºC) |
| Коричневый | 100 |
| Красный | 50 |
| Желтый | 25 |
| Оранжевый | 15 |
| Голубой | 10 |
| Фиолетовый | 5 |
| Белый | 1 |
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Резисторы поверхностного монтажа на печатной плате
Автор статьи: Анатолий Золотков
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Читайте также: Как соединить чайник напрямую. Как отремонтировать дисковый электрочайник. Ослабленное крепление нагревательного элемента
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Паяльная станция 2 в 1 с ЖК-дисплеемМощность: 800 Вт, температура: 100…480 градусов, поток возду…Подробнее
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Простые примеры расчета
Бытовая сеть переменного тока
Пример №1. Проверка ТЭНа.
В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления. По мощности рассчитываем ток и сопротивление.
I = 1250 / 220 = 5,68 А; R = 220 / 5,68 = 38,7 Ом.
Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.
Пример №2. Проверка сопротивления двигателя
Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии. Считаем ток:
I = 1600 / 220 = 7,3 А.
Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:
- сопротивление двигателя — 30,1 Ома;
- мощность 1600 ватт.
Цепи постоянного тока
Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.
Считаем ток:
I = 55 / 12 = 4,6 А.
Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:
- сопротивление 2,6 ома.
- мощность 5 ватт.
Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже.
Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.
Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.
Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.
В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.
При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.
Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.
Читайте также: Какими характеристиками обладает датчик движения IEK?
Смешанное подключение
В этом случае на участке схемы используется комбинация параллельного и последовательного включения элементов. Такое соединение часто называется параллельно-последовательным:
- При последовательном включении общий импеданс элементов прямо пропорционален сумме сопротивлений каждого из резисторов.
- При параллельном включении проводников значение, обратное сумме импеданса цепи, соответствует сумме значений, обратных сопротивлениям параллельно включённых элементов.

Используя эти правила, которые справедливы для любого числа соединённых проводников в схеме, определяется общее значение импеданса для любого вида подключения. Для того чтобы определить эквивалентное значение сопротивления параллельно-последовательного соединения, участок схемы делится на небольшие группы из параллельно или последовательно включённых резисторов. Затем используется алгоритм, помогающий оптимально посчитать значение эквивалента:
Определяется общее сопротивление всех узлов в схеме с параллельным подключением резисторов:
- При нахождении в этих узлах последовательно соединённых проводников первоначально считается их сопротивление.
- Как только значения эквивалентных значений вычислены, схема упрощается до последовательной цепочки из эквивалентных резисторов.
- Находится окончательное значение общего сопротивления.
Например, существует схема, в которой надо определить полное сопротивление цепи, при этом сопротивление резисторов R1=R3=R5=R6=3 Ом, а R2 =20 Ом и R4=24 Ом. Сопротивления R3, R4, и R5 включены последовательно, поэтому общий импеданс на этом участке цепи равен: Rоб1 = R3+R4+R5 = 30 Ом.
После замены R3, R4, R5 на Rоб1 резистор R3 окажется подключённым параллельно этому сопротивлению. Поэтому импеданс на этом участке будет равен:
Rоб2 = (R2* Rоб1) / (R3+Rоб1) = (20*30) / (20+30) = 12 Ом.
Резисторы R1 и R6 включены с Rоб2 последовательно, а это значит, что эквивалент всей схемы равен: Rэкв = Rоб1+Rоб2+ R6 = 3+12+3 = 18 Ом.
Так шаг за шагом вычисляется эквивалентное значение любой сложности схемы. При множестве проводников, входящих в электрическую цепь, нетрудно ошибиться при расчётах, поэтому все операции выполняются аккуратно или используются онлайн-калькуляторы.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Параллельное соединение проводников
Параллельное соединение, каких-либо компонентов, например, резисторов в схеме выглядит приблизительно как на схеме ниже:

Рис. 2. Параллельное соединение резисторов
По аналогии с двумя проводниками, соединенными параллельно, мы также можем нарисовать прямоугольник шире. Сопротивление становится меньше. Применяется следующая формула:
1 / Rобщ = 1 / R1 + 1 / R2 , отсюда:
Rобщ = ( R1 * R2 ) / (R1 + R2) (примечание — на рисунке Rобщ = Rges )
Если у нас N проводников соединено параллельно, тогда формула примет вид:
1 / Rобщ = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / RN, то есть чем больше в электрической цепи подключено проводников, тем меньше будет общее сопротивление.
В каждом ответвлении ток I разделяется на I1, I2, … IN. Это приводит к следующим соотношениям:
- Iобщ = I1 + I2 + I3 + … + IN
- Uобщ = U1 = U2 = U3 = … = UN
В электрической цепи с параллельным соединением проводников напряжение постоянно, а электрический ток можно сложить до общего тока путем сложения отдельных токов на каждом из проводников.
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Параллельное соединение: общая информация
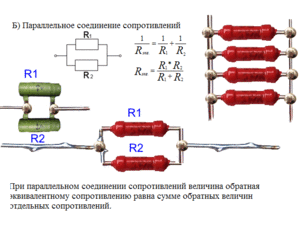
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет общего сопротивления для параллельного соединения
Примечание: Вы можете увеличить количество резисторов, подключенных последовательно или параллельно.
Последовательное соединение светодиодов
Часто несколько светодиодов подключают последовательно к одному источнику напряжения. При последовательном соединении одинаковых светодиодов их общий ток потребления равняется рабочему току одного светодиода, а общее напряжение равно сумме напряжений падения всех светодиодов в цепи.

Поэтому, в данном случае, нам достаточно использовать один резистор для всей последовательной цепочки светодиодов.
Пример расчета сопротивления резистора при последовательном подключении.
В этом примере два светодиода соединены последовательно. Один красный светодиод с напряжением 2В и один ультрафиолетовый светодиод с напряжением 4,5В. Допустим, оба имеют номинальную силу тока 30 мА.

Из правила Кирхгофа следует, что сумма падений напряжения во всей цепи равна напряжению источника питания. Поэтому на резисторе напряжение должно быть равно напряжению источника питания минус сумма падения напряжений на светодиодах.
Используя закон Ома, вычисляем значение сопротивления ограничительного резистора:
Резистор должен иметь значение не менее 183,3 Ом.
Обратите внимание, что после вычитания падения напряжений у нас осталось еще 5,5 вольт. Это дает возможность подключить еще один светодиод (конечно же, предварительно пересчитав сопротивление резистора)
Параллельное соединение

Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку. В этом случае напряжение на всех элементах одинаковое, а проходящая сила тока зависит от их импеданса.
Формула параллельного соединения резисторов выглядит следующим образом:
R = (R1*R2*R3…*Rх) / (R1+R2+R3…+Rх), где Rх – порядковый номер резистора.
Отсюда следует, что сила тока, протекающая через каждый проводник, находится по формуле: In = U/Rn.
Исходя из этого, при параллельном соединении результирующий импеданс двух и более резисторов будет меньше самого меньшего значения сопротивления в соединении. При этом когда параллельно включены только два резистора, имеющие одинаковый номинал, то их можно заменить эквивалентом, равным одной второй от величины этого номинала.
Так можно соединить и сотню резисторов, тогда эквивалентное сопротивление определяется как сотая часть от номинала. Например, пусть будет участок схемы с десятью резисторами, включёнными параллельно друг другу с номиналом каждого равного 10 Ом, тогда общее сопротивление будет составлять десятую часть, а именно Rоб = 10/10 = 1 Ом.
Важно отметить, что при таком соединении величина тока поделится на каждый элемент, поэтому и резисторы можно применить меньшей мощности, чем если бы использовался эквивалент, заменяющий всё параллельное подключение.
Читайте также: Порядок монтажа и подключения блока питания 12в для светодиодной ленты
Пример подбора замены
При разработке прибора возникла потребность использовать на участке цепи резистор с сопротивлением 6 Ом. При изучении номинального ряда стандартных значений, выпускаемых промышленностью, можно отметить, что резистора на 6 Ом в нём нет.
Для получения нужного значения понадобится воспользоваться параллельным включением двух элементов. Эквивалентное значение сопротивления для двух резисторов в таком случае находится в следующем порядке:
- 1/R = (1/R1) + (1/R2);
- 1/R = (R1+R2) / (R1*R2);
- Rэ = (R1*R2) / (R1+R2).
Из решения видно, что если R1 совпадает по номиналу с R2, то общая величина сопротивления равна половине значения одного из элементов. Поэтому при требуемом номинале, равном 6 Ом, это значение составит: Rx = 2*6 = 12 Ом. Для проверки результата следует подставить полученный ответ в формулу: Rэ = (R1*R2) / (R1+R2) = (12*12) / (12+12) = 6 Ом.
Таким образом, решением поставленной задачи будет параллельное включение двух резисторов с величиной сопротивления, равной 12 Ом.
Задача на нахождение эквивалента
Пусть существует схема с тремя параллельно включёнными резисторами и для её упрощения необходимо заменить их одним элементом. Номиналы проводников составляют: R1 = 320 Ом, R2= 10 Ом, R3 = 1 кОм. Для решения задачи используется уже известная формула:
- 1/R = (1/R1) + (1/R2) + (1/R3);
- Rэкв = (R1*R2*R3) / (R1+R2+R3).
Перед тем как подставлять величины в формулу, их все понадобится привести к международной системе единиц (СИ). Так, один килоОм равен 1000 Ом, при подставлении этого значения получается ответ: Rэ = (320*1*1000) / (320+10+1000) = 2406 Ом или 2,4 кОм, что как раз соответствует величине из стандартного ряда. Такая методика расчёта применяется для любого количества параллельно соединённых резисторов.
Можно ли обойтись без резисторов
В бюджетных или просто старых приборах используются резисторы. Также они используются для подключения всего только нескольких светодиодов.
Но есть более современный способ – это понижение тока через светодиодный драйвер. Так, в светильниках в 90% встречаются именно драйверы. Это специальные блоки, которые через схему преобразуют характеристики тока и напряжения питающей сети. Главное их достоинство – они обеспечивают стабильную силу тока при изменении/колебании входного напряжения.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.
Видео

Кофе в капсулах Nescafe Dolce Gusto Cappuccino, 8 порций (16 капсул)
435 ₽ Подробнее

Кофе капсульный Nescafe Dolce Gusto Кафе О Ле Кофе с молоком, 3 упаковки по 16 капсул
1305 ₽ Подробнее
Лучшие планшеты
Пример расчёта
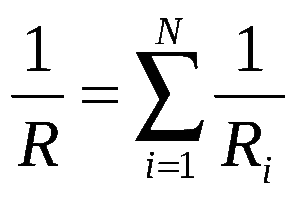
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Читайте также: Что такое карбид. Свойства карбида. Применение карбида
Электри́ческое сопротивле́ние
— физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R
или
r
) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U
— разность электрических потенциалов (напряжение) на концах проводника;
I
— сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении
проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U
1 и
U
2 на проводниках равны
Общее напряжение U
Читайте также: Пневмодомкрат автомобильный: конструкция, варианты изготовления своими руками
на обоих проводниках равно сумме напряжений
U
1 и
U
2:
где R
– электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении
(рис. 1.9.2) напряжения
U
1 и
U
2 на обоих проводниках одинаковы:
Сумма токов I
1 +
I
2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A
и
B
) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу
A
за время Δ
t
подтекает заряд
I
Δ
t
, а утекает от узла за то же время заряд
I
1Δ
t
+
I
2Δ
t
. Следовательно,
I
=
I
1 +
I
2.
Читать также: Какое отверстие сверлить под дюбель 8 мм

Параллельное соединение проводников
Записывая на основании закона Ома
где R
– электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Читайте также: Виды и особенности бит для шуруповерта
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Практический пример
Рассмотрим пример-задачу, чтобы на практике увидеть, как можно применить формулы последовательного и параллельного соединения проводников, в качестве которых выступают резисторы.
Входные данные у нас следующие:
- Напряжение источника питания U0 = 120 В;
- R1 = 150 Ом, R2 = 62,5 Ом, R3 = 250 Ом.
Нам нужно найти:
Rобщ, Iобщ , I1, I2, I3, U1, U2, U3 и U23.

Электрическая цепь
Сначала рассчитаем общее сопротивление R23 параллельной электрической цепи, которую образуют резисторы R2 и R3:
R23 = ( R2 * R3 ) / (R2 + R3) = (62,5 * 250) / (62,5 + 250) = 50 Ом.
Теперь можно мысленно заменить участок из параллельно соединенных резисторов R2 и R3 одним общим сопротивлением R23, который в свою очередь с R1 будет уже образовывать электрическую цепь с последовательным соединением резисторов. И мы, следовательно, можем рассчитать общее сопротивление:
Rобщ = R1 + R23 = 50 + 150 = 200 Ом.
Теперь мы можем рассчитать общий ток Iобщ этой последовательной электрической цепи, равный одновременно электрическому току I1 протекающему через резистор R1, используя закон Ома:
Iобщ = U0 / Rобщ = 120 / 200 = 0,6 А = I1.
Теперь мы можем рассчитать напряжение U1 на резисторе R1 и общее напряжение U23 в параллельной электрической цепи, состоящей из резисторов R2 и R3:
U1 = R1*I1 = 150 * 0,6 = 90 В.
А так как U0 = U1 + U23, то получаем U23 = U0 — U1 = 120 — 90 = 30 В = U2 = U3.
Наконец, мы вычисляем I2 и I3 :
I2 = U2 / R2 = 30 / 62,5 = 0,48 А
I3 = U3 / R3 = 30 / 250 = 0,12 А.