Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

[quads id=1]

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют несколько факторов.

Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками

Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах

Автор статьи: Анатолий Золотков

Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:

Калькулятор резистивно-емкостной цепи

Калькулятор параллельных сопротивлений

Калькулятор параллельных индуктивностей

Калькулятор емкости последовательного соединения конденсаторов

Калькулятор импеданса конденсатора

Калькулятор импеданса катушки индуктивности

Калькулятор взаимной индукции

Калькулятор взаимоиндукции параллельных индуктивностей

Калькулятор взаимной индукции — последовательное соединение индуктивностей

Калькулятор импеданса параллельной RC-цепи

Калькулятор импеданса параллельной LC-цепи

Калькулятор импеданса параллельной RL-цепи

Калькулятор импеданса параллельной RLC-цепи

Калькулятор импеданса последовательной RC-цепи

Калькулятор импеданса последовательной LC-цепи

Калькулятор импеданса последовательной RL-цепи

Калькулятор импеданса последовательной RLC-цепи

Калькулятор аккумуляторных батарей

Калькулятор литий-полимерных аккумуляторов для дронов

Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC)

Калькулятор расчета параметров коаксиальных кабелей

Калькулятор светодиодов. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов

Калькулятор цветовой маркировки резисторов

Калькулятор максимальной дальности действия РЛС

Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов

Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС

Калькулятор радиогоризонта

Калькулятор эффективной площади антенны

Симметричный вибратор

Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации

Калькулятор мощности постоянного тока

Калькулятор мощности переменного тока

Калькулятор пересчета ВА в ватты

Калькулятор мощности трехфазного переменного тока

Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую

Калькулятор коэффициента гармонических искажений

Калькулятор законов Ома и Джоуля — Ленца

Калькулятор времени передачи данных

Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора

Калькуляторы Электротехнические и радиотехнические калькуляторы

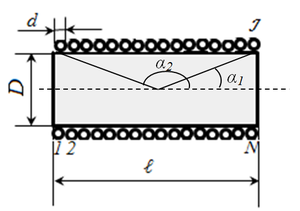
Соленоид

Соленоид отличается от обычной катушки по двум признакам:

• Длина обмотки превышает диаметр в несколько раз;
• Толщина обмотки меньше диаметра катушки также в несколько раз.

Соленоидальный тип катушки

Параметры соленоида можно узнать из такого выражения:

L=µ0N2S/l,

где:

• µ0 – магнитная постоянная;
• N – количество витков;
• S – площадь поперечного сечения обмотки;
• l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника.

Обратите внимание! Используя подвижный сердечник, можно производить оперативное изменение параметров соленоида.

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Вам это будет интересно  Как работает схема триггера на транзисторах

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

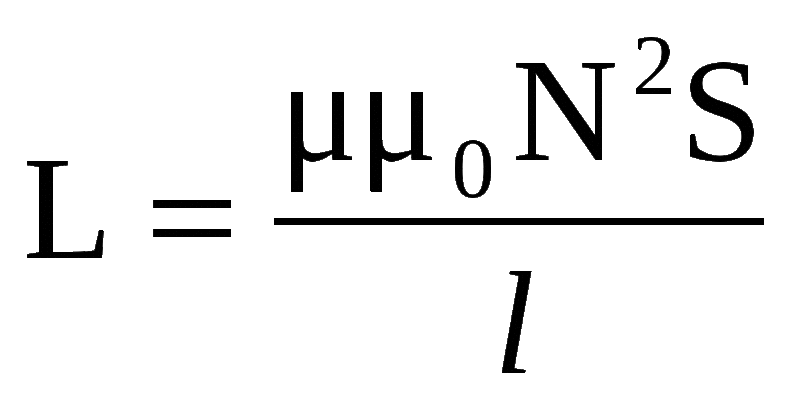
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• 
  µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Вам это будет интересно  Все об статиче6ском электричестве

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• 
  l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Колебательный контур

Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.

Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.

Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

• L= µ0n2V,

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

• L = µ0N2S : l,

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Тороидальная катушка (катушка с кольцевым сердечником)

Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:

где r – усредненный радиус тороидального сердечника.

Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:

где:

r – внутренний радиус сердечника;

R – внешний радиус;

Важно! Вторая формула позволяет узнавать результат с большей точностью.

Длинный прямой проводник

Как найти индуктивность прямого проводника? Существует формула, дающая точное значение при условии, что проводник имеет длину, значительно превышающую толщину:

L=µ0/(2π)∙l(µeln(l/r+1/4µi),

где:

• µe и µi – магнитная проницаемость среды и материала проводника, соответственно;
• l и r – длина и радиус проводника.

Какой магнитной проницаемостью обладает проводник, можно узнать из справочных материалов.

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Вам это будет интересно  Особенности конденсатора

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Индуктивное сопротивление – как его найти

Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:

XL=2*П*v*L

Здесь употреблены следующие обозначения:

1. XL – рассматриваемая величина.
2. Символом «П» обозначено число Пи.
3. V представляет собой частоту.
4. L — это обозначение величины индуктивности.

Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».

Катушки с различными сердечниками

Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:

I = U / XL

I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.

Конфигурация магнитного поля катушки

Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.

При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.

Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.

Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.

Магнитное поле провода

К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.

Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.

При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.

Советуем изучить Антенна для автомагнитолы

Электрическая цепь и индуктивность

Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.

Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.

Расчет катушки в броневом ферритовом сердечнике

Ферритовые сердечники для катушек индуктивности бывают самыми разнообразными. Ш-образные, П-образные, броневые разных модификаций. Кроме феррита для таких сердечников используют и порошковые материалы, карбонильное железо. Расчет катушек на таких сердечниках можно вести разными способами. На Западе при расчете катушек с любым ферритовым сердечником принят способ расчета через специальный параметр AL и расчет ведется по таким же формулам как и для ферритовых колец.

Читайте также:  Комплект заземления для частного дома и дачи — универсальные наборы от 6 до 15 метров на базе оцинкованных, омеднённых стержней и стержней из нержавеющей стали для установки качественного заземления с

Основная формула расчета:

• L — индуктивность (нГн)
• AL -коэффициент индуктивности сердечника (нГн/виток в квадрате)
• N — число витков катушки

Параметр AL можно найти в спецификациях производителя.

Однако не все производители публикуют значения AL для своих сердечников. В таком случаем вы можете рассчитать катушку если вам известны физические размеры сердечника и его магнитная проницаемость.

Метод расчета, который использует Coil64, рекомендован к использованию Международной Ассоциацией Производителей Магнитных Материалов в публикации: IEC Publication 205, “Calculation of Effective Parameters of Magnetic Piece Parts.” В этом методе броневой сердечник заменяется на идеальный тороидальный сердечник, на такой который имеет такие же электрические параметры и содержит столько же витков как и оригинальный броневой сердечник. Параметры магнитной цепи такого замещающего тороидального сердечника называются эффективными. Этот факт отображается добавкой суффикса “e” к соответствующему символу.

1. Эффективная длина магнитной цепи le мм
2. Эффективное поперечное сечение магнитной цепи Ae мм2
3. Эффективный объем сердечника Ve mm3

Для того чтобы рассчитать эти параметры, закрытая магнитная цепь броневого сердечника делится на пять секций. Для каждой секции отдельно рассчитывается эффективное поперечное сечение и длина магнитной цепи.

1. Первым шагом определяем первичные параметры для расчета на основе данных измерений или размеров из даташита: h = (h1 — h2) / 2; r1 = D4 / 2; r2 = D3 / 2; r3 = D2 / 2; r4 = D1 / 2
2. Влияние пазов b на конечный результат учитывается поправочными коэффициентами k1, k2, k3, где n число пазов:
3. Длина магнитной цепи по внешнему кольцу: l1 = h2. Площадь поперечного сечения этого кольца A1 = A’1 + A»1 при условии A’1 = A»1 равна:
4. Длина магнитной цепи центрального керна: l3 = h2. Площадь его поперечного сечения A3 = A’3 + A»3 при условии A’3 = A»3 равна:
5. Длина магнитной цепи верхней и нижней плоских частей сердечника l2 = l’2 + l»2, соотношения, требуемые для расчета констант С1 и С2 сердечника:
6. Дополнительные уравнения для соблюдения условий A’1 = A»1 и A’3 = A»3 и для нахождения длины магнитного пути угловых секций l4 = l’4 + l»4 и l5 = l’5 + l»5 следующие:
7. Средняя длина магнитной цепи угловых секций:
8. Площадь поперечного сечения ассоциированная с путями l4 и l5:
9. Расчетные константы для полной длины магнитной цепи броневого сердечника определяются следующим образом:
10. Зная эти константы мы можем определить эффективные параметры сердечника le [мм], Ae [мм2], Ve [мм3]:
11. Чтобы учесть влияние зазора в магнитной цепи в центральном керне, который имеет высокое магнитное сопротивление, сердечник с зазором заменяется виртуальным сердечником без зазора с таким же числом витков, но с меньшей проницаемостью. Магнитная проницаемость такого замещающего сердечника называется эффективной магнитной проницаемостью:где µr — реальная магнитная проницаемость сердечника. Когда катушка работает в режиме малого сигнала, эту величину можно принять равной начальной магнитной проницаемости сердечника µi.
12. В итоге на основе вычисленных эффективных параметров мы можем определить искомую индуктивность катушки в броневом сердечнике:где:

• L — индуктивность [мГн];
• µ0 = 4 π · 10-7 — магнитная константа [Гн/м];
• µe — эффективная магнитная проницаемость сердечника;
• N — число витков;
• Ae — эффективная площадь поперечного сечения магнитной цепи [мм2];
• le — эффективная длина магнитной цепи [мм];

Допустимые отклоненя значений µi достаточно велики, кроме того есть зависимость магнитной проницаемости от температуры. Для сердечников без зазора большое значение имеет неплотность прилегания половинок сердечника друг к другу. Даже при очень малом образующемся при этом зазоре, порядка 0,01 мм, эффективная магнитная проницаемость значительно ниже начальной. Учитывая вышесказанное, приходим к выводу что данный метод расчета индуктивности катушек в броневом сердечнике может давать погрешность до ±30% и выше и может быть использован для сердечников с неизвестным AL. Для более точных расчетов нужно использовать значения AL, если они есть в даташитах производителя.

Ссылки по теме:

1. — The International Magnetics Association 2011 (PDF);
2. — Начинающим, Силовая электроника — авторский блог;

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt

u = Uм sin (ϕ + ωt),

e = Ɛm sin (ψ + ωt).

Читайте также:  Сетевой фильтр – что это такое, отличие от удлинителя, основные виды устройства

Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:

R=(pl/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

График и схема подключения

Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

ХL = ωL.

Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Катушки индуктивности

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

Будет интересно➡ Что такое элемент Пельтье и как его сделать своими руками?

X = XL—XC

и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I2R

Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при XL=XC.)

Индуктивность

Ресчет катушек индуктивности (однослойных, цилиндрических)

Рис. 1. Пример однослойной катушки индуктивности.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников. Расчет однослойных цилиндрических катушек производится по формуле:

где:

• L — индуктивность катушки, мкГн;
• D — диаметр катушки, см;
• I — длина намотки катушки, см;
• n — число витков катушки.

При расчете катушки могут встретиться два случая:

• а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
• б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 1; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода.

Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле:

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле:

где:

• d — диаметр провода, мм,
• l — длина обмотки, мм,
• n — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины, получим:

Диаметр провода:

Если эту катушку наматывать проводом меньшего диаметра, то нужио полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки.

Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки.

Возможно, также придется увеличить и то и другое одновременно, пока не будут получепы необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным пыше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше D половины диаметра то более точные результаты можно получить по формулам:

Дроссель

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Многовитковые и одновитковые катушки

От чего зависит индуктивность катушки? Во многом она связана с кол-вом витков вокруг сердечника.

В одновитковом контуре используется формула, которая определяет характеристику через ампераж и электромагнитный поток.

Выглядит она так:

Ф/I

В многовитковых катушках этот же параметр равен квадрату каждого витка, т.к. увеличивается потокосцепление:

L1 х N2.

Для правильного расчета многовитковых катушек учитывается так же геометрические параметры и намоточный тип.

Обозначение и единицы измерения

В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.

Как может обозначаться индуктивность в других системах:

• В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
• В системе СГСЭ – в статгенри.

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

• сглаживание пульсаций и помех, накопление энергии;
• создание магнитных полей в различных устройствах;
• фильтры цепей обратной связи;
• создание колебательных контуров;
• трансформаторы (устройство из двух катушек, связанных индуктивно);
• силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
• ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
• применение катушек в качестве электромагнитов различных исполнительных механизмов;
• обмотки электромагнитных реле;
• индукционные печи;
• установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Свойства

Имеет следующие свойства:

• Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
• Не может быть отрицательной;
• Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
• При увеличении частоты тока реактивное сопротивление катушки увеличивается;
• Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.