Энергия заряженного конденсатора
Чему будет равен максимальный заряд конденсатора
Колебательный контур, состоящий из катушки индуктивности и конденсатора, настроен на длину волны м . Если максимальный ток в цепи I=0,02 А, то максимальный заряд конденсатора равен ———————————————————————————————————————-
где: — скорость распространения электромагнитного поля (на сколько я понял в данном случае в вакууме) — индуктивность контура — ёмкость контура
где: I-максимальная сила тока в контуре w — циклическая частота q — амплитудное значение заряда
из формулы 1) можно найти зная можно найти «q — амплитудное значение заряда» «q — амплитудное значение заряда» это и будет «максимальным зарядом конденсатора» ?
Чему равен модуль Юнга Магнитофонная лента имеет толщину d=5 мкм и ширину b=5 мм. Если к ленте длиной L=0.7 м подвесить.
Чему равен наибольший потенциал Чему равен наибольший потенциал, приобретаемый отрицательно заряженной металлической пластинкой .
Читайте также: § 13. ЭДС индукции в движущихся проводниках
Чему равен период колебаний частицы? Прошу распишите как решать эти задаче никак не могу их решить Задача 1 Частица, совершающая.
Чему равен радиус диска, если период его колебаний 2 с? на гвозде, вбитом в стену, висит диск так, что точка подвеса находится на расстоянии 1/6 радиуса от.
Источник
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что








Конденсатор

Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).
Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).
- 1nF = 0.000000001 = 10-9 F
- 1pF = 0.000000000001 = 10-12 F
Плоский конденсатор
Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).
Заряд конденсатора. Ток
По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.






1.7. Энергия электрического поля
Опыт показывает, что заряженный конденсатор содержит запас энергии.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу
Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:
| Рисунок 1.7.1. Процесс зарядки конденсатора |
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.
Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)
где k – жесткость пружины, x – деформация, F = kx – внешняя сила.
По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.
Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость Поэтому
где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.
Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.
Как правильно рассчитать ёмкость конденсатора?
Самый простой пример конденсатора – плоская модель. Она имеет форму двух параллельных крышек из проводника, между которыми находится слой диэлектрика. Для того, чтобы знать, как посчитать ёмкость конденсаторов, необходимо применить следующую формулу:
С = e x e0 x s / d,
где S – площадь поверхности пластинок и d – расстояние между ними. В свою очередь, это относительная электрическая проницаемость данного диэлектрика.
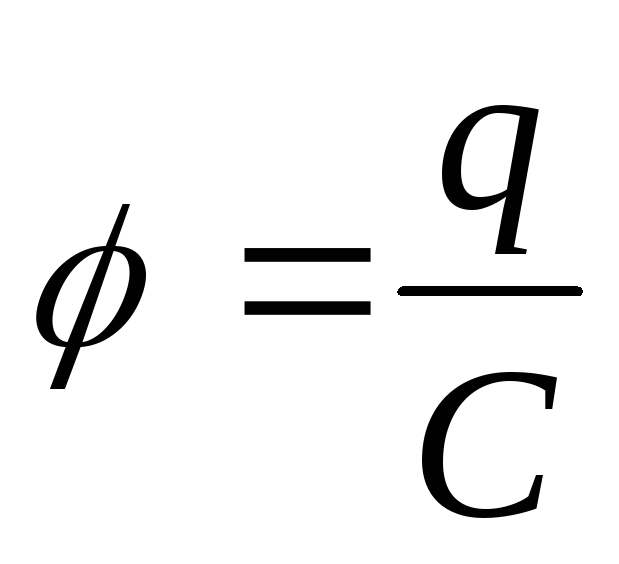





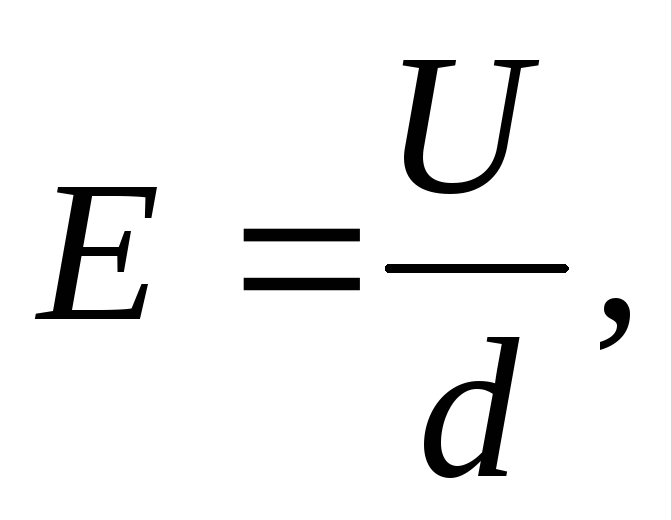





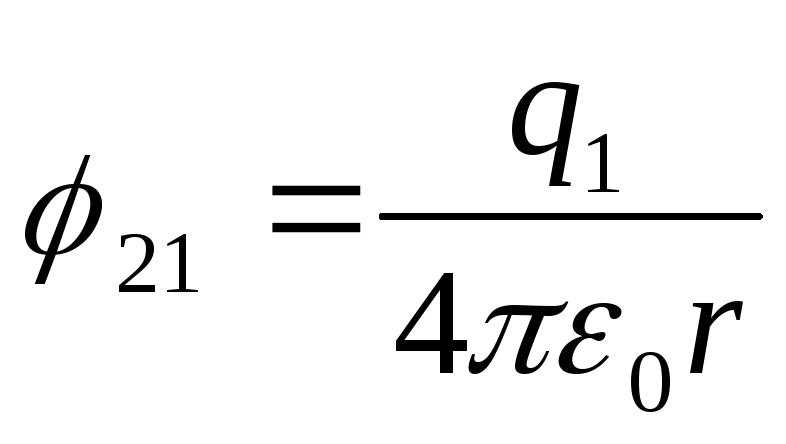




Как правило, конденсаторы применяются не по отдельности, а подключаются в более крупные системы. Они могут быть соединены последовательно, параллельно или смешанным способом.


Формула ёмкости
Важно! В последовательно соединённых элементах абсолютное значение заряда на каждой пластине идентично. Таким образом, результирующее напряжение равно сумме данных показателей на отдельных компонентах прибора
Таким образом, результирующее напряжение равно сумме данных показателей на отдельных компонентах прибора.
Общая ёмкость системы будет определяться по формуле:
1/С = 1/С1 + 1/С2 + 1/С3 + …
При параллельном подключении разность потенциалов на каждом из деталей одинакова. Таким образом, суммарный заряд будет равен сумме зарядов на компонентах конденсатора, а результирующая ёмкость – сумме отдельных единичных величин:
C = c1 + c2 + c3 + …
Примеры решения задач
Пример 12. 5.
К пластинам плоского воздушного конденсатора приложена разность потенциалов 1,5 кВ. Площадь пластин 150см2и расстояние между ними 5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами вставили стекло (ε2=7).Определите:
1) разность потенциалов между пластинами после внесения диэлектрика; 2) ёмкость конденсатора до и после внесения диэлектрика; 3) поверхностную плотность заряда на пластинах до и после внесения диэлектрика.
Дано
: U 1 =1,5кВ=1,5∙10 3 В; S=150см 2 =1,5∙10 -2 м 2 ; ε 1 =1; d=5мм=5∙10 -3 м.
Читайте также: Формула напряженности магнитного поля
Найти: 1)
U 2 ; 2) С 1 С 2 ; 3) σ 1 , σ 2
Решение
.
Так как (σ- поверхностная плотность зарядов на обкладках конденсатора), то до внесения диэлектрика σd=U 1 ε 0 ε 1 и после внесения диэлектрика σd=U 2 ε 0 ε 2 , поэтому
Ёмкость конденсатора до и после внесения диэлектрика
и
Заряд пластин после отключения от источника напряжения не меняется, т.е. q=const. Поэтому Поверхностная плотность заряда на пластинах до и после внесения диэлектрика
Ответ: 1) U 2 =214В; 2) С 1 =26,5пФ; С 2 =186пФ; 3) σ 1 = σ 2 =2.65 мкКл/м 2 .
Пример 12.7. Зазор между обкладками плоского конденсатора заполнен анизотропным диэлектриком, проницаемость ε которого изменяется в перпендикулярном к обкладкам направлении по линейному закону
ε = α + βх
от ε1до ε2, причём ε2> ε1. Площадь каждой обкладкиS, расстояние между нимиd. Найти ёмкость конденсатора.
Дано
: S; d; ε 1 ; ε 2
Найти:
С.
Решение
.
Диэлектрическая проницаемость
ε
изменяется по линейному закону, ε = α + βх, где х отсчитывается от обкладки, у которой проницаемость равна ε 1 . Учитывая, что ε (0) = ε 1 , ε (d) = ε 2 , получаем зависимость . Найдём разность потенциалов между обкладками:
Ёмкость конденсатора будет равна
Ответ:
Читайте также: Конспект урока по физике на тему: «Последовательное соединение проводников» в 8 классе
Пример 12.7. Между пластинами плоского конденсатора, заряженного до разности потенциалов
U, параллельно его обкладкам помещены два слоя диэлектриков. Толщина слоёв и диэлектрическая проницаемость диэлектриков соответственно равныd1,d2, ε1, ε2. Определите напряжённость электростатических полей в слоях диэлектриков.
Дано
:
U
Найти:
E 1 , E 2 .
Решение
.
Напряжение на пластинах конденсатора, учитывая, что поле в пределах каждого из диэлектрических слоёв однородно,
U=E 1 d 1 +E 2 d 2 . (1)
Электрическое смещение в обоих слоях диэлектрика одинаково, поэтому можем записать
D=D 1 =D 2 = ε
0ε1
E 1 =
ε0ε2
E 2 (2)
Из выражения (1) и (2) найдём искомое
(3)
Из формулы (2) следует, что
Ответ:
Пример 12.7. Площадь пластин
Sплоского конденсатора равна 100см2. Пространство между пластинами заполнено вплотную двумя слоями диэлектриков – слюдяной пластинкой (ε1=7) толщинойd1=3,5 мм и парафина (ε2=2) толщинойd2=5 мм. Определите ёмкость этого конденсатора..
Дано
:
S=100см2=10-2м2; ε1=7;d1=3,5мм=3.5∙10-3м;, ε1=2;d1=3,5мм=5∙10-3м;
Найти:
С.
Решение
.
Ёмкость конденсатора
где = — заряд на пластинах конденсатора (- поверхностная плотность заряда на пластинах); =- разность потенциалов пластин, равная сумме напряжений на слоях диэлектрика: U=U 1 +U 2 . Тогда
(1)
Напряжения U 1 и U 2 найдём по формулам
где Е 1 и Е 2 – напряжённость электростатического поля в первом и втором слоях диэлектрика; D — электрическое смещение в диэлектриках (в обоих случаях одинаково). Приняв во внимание, что
И учитывая формулу (2), из выражения (1) найдём искомую ёмкость конденсатора
Ответ:
С=29,5пФ.
Пример 12.7. Батарея из трёх последовательно соединённых конденсаторов С
1=1мкФ; С2=2мкФ и С3=4мкФ подсоединены к источнику ЭДС. Заряд батареи конденсаторовq=40мкКл. Определите: 1) напряженияU1,U2иU3на каждом конденсаторе; 2) ЭДС источника; 3) ёмкость батареи конденсаторов.
Дано
:
С 1 =1мкФ=1∙10 -6 Ф; С 2 =2мкФ=2∙10 -6 Ф и С 3 =4мкФ=4∙10 -6 Ф;q=40мкКл=40∙10 -6 Ф
.
Найти: 1)
Читайте также: Общие сведения о технологии авиадвигателестроения
U 1 , U 2 , U 3 ; 2) ξ; 3) С.
Решение
.
При последовательном соединении конденсаторов заряды всех обкладок равны по модулю, поэтому
q 1 =q 2 =q 3 =q.
Напряжение на конденсаторах
ЭДС источника равна сумме напряжений каждого из последовательно соединённых конденсаторов:
ξ = U 1 + U 2 +U 3
При последовательном соединении суммируются величины, обратные ёмкостям каждого из конденсаторов:
Откуда искомая ёмкость батареи конденсаторов
Ответ: 1)
U 1 = 40В; U 2 = 20В, U 3 = 10В; 2) Ɛ= 70В; 3) С= 0,571мкФ.
Пример 12.7. Два плоских воздушных конденсатора одинаковой ёмкости соединены последовательно и подключены к источнику ЭДС. Как и во сколько раз изменится заряд конденсаторов, если один из них погрузить в масло с диэлектрической проницаемостью ε=2,2 .
Дано
: С 1 =С 2 = С;q=40мкКл=40∙10 -6 Ф

.
Решение
.
При последовательном соединении конденсаторов заряды обоих конденсаторов равны по модулю. До погружения в диэлектрик (в масло) заряд каждого конденсатора
где ξ = U 1 + U 2 (при последовательном соединении конденсаторов ЭДС источника равна сумме напряжений каждого из конденсаторов).
После погружения одного из конденсаторов в диэлектрик заряды конденсаторов опять одинаковы и соответственно на первом и втором конденсаторах равны
q= CU 1 =ε 2 CU 2
(учли, что ε 1 =1), откуда, если учесть, что ξ = U 1 + U 2 , найдём
(2)
Поделив (2) на (1), найдём искомое отношение
Ответ:
, т.е. заряд конденсаторов возрастает в 1,37 раз.
Пример 12.7. Конденсаторы ёмкостями С каждый соединены так, как указано на рис.а. определите ёмкость С
общэтого соединения конденсаторов. .
Решение
.
Если отключить от цепи конденсатор С 4 , то получится соединение конденсаторов, которое легко рассчитывается. Поскольку ёмкости всех конденсаторов одинаковы (С 2 =С 3 и С 5 =С 6), обе параллельные ветви симметричны, поэтому потенциалы точек А и В, одинаково расположенные в ветвях, должны быть равны. Конденсатор С 4 подключен, таким образом, к точкам с нулевой разностью потенциалов. Следовательно, конденсатор С 4 не заряжен, т.е. его можно исключить и схему, представленную в условии задачи, упростить (рис.б).
Эта схема- из трёх параллельных ветвей, две из которых содержат по два последовательно включённых конденсаторов
Ответ:
С общ =2С.
Пример 12.7.
Плоский воздушный конденсатор ёмкостью С1=4пФ заряжен до разности потенциаловU1=100В. После отключения конденсатора от источника напряжения расстояние между обкладками конденсатора увеличили в два раза. Определите: 1) разность потенциаловU2на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин.
Дано
: С 1 =4пФ=4∙10 -12 Ф; U 1 =100В;d 2 =2d 1 .
Найти:
1) U 2 ;2)A.
Решение
.
Заряд обкладок конденсатора после отключения от источника напряжения не меняется, т.е. Q=const. Поэтому
С 1 U 1 = С 2 U 2 , (1)
где С 2 и U 2 — соответственно ёмкость и разность потенциалов на обкладках конденсатора после их раздвижения.
Учитывая, что ёмкость плоского конденсатора , из формулы (1) получим искомую разность потенциалов
(2)
После отключения конденсатора от источника напряжения систему двух заряженных обкладок можно рассматривать как замкнутую, для которой выполняется закон сохранения энергии: работа А внешних сил равна изменению энергии системы
А= W 2 — W 1 (3)
где W 1 и W 2 – соответственно энергия поля конденсатора в начальном и конечном состояниях.
Учитывая, что и (q – const), из формулы (3) получим искомую работу внешних сил
Читайте также: Tl431 расчет делителя напряжения для импульсного бп
[учли, что q=C 1 U 1 и формулу (2)].
Ответ
: 1) U 2 =200В;2)A=40нДж.
Пример 12.7.
Сплошной шар из диэлектрика радиусомR=5см заряжен равномерно с объёмной плотностью ρ=5нКл/м3. Определите энергию электростатического поля, заключённую в окружающем шар пространстве.
Дано
: R=5см=5∙10 -2 м;
ρ=5нКл/м3=
5∙10 -9 Кл/м 3 .
Найти:
W.
Решение
.
Поле заряженного шара сферически симметрично, поэтому объёмная плотность заряда одинакова во всех точках, расположенных на равных расстояниях от центра шара.
Энергия в элементарном сферическом слое (он выбран за пределами диэлектрика, где следует определить энергию) объёмомdV (см. рисунок)
где dV=4πr 2 dr (r – радиус элементарного сферического слоя; dr — его толщина); (ε=1 – поле в вакууме; Е – напряженность электростатического поля).
Напряжённость Е найдём по теореме Гаусса для поля в вакууме, причём в качестве замкнутой поверхности мысленно выберем сферу радиусом r (см. рисунок). В данном случае внутрь поверхности попадает весь заряд шара, создающий рассматриваемое поле, и, по теореме Гаусса,
Откуда
Подставив найденные выражения в формулу (1), получим
Энергия, заключённая в окружающем шар пространстве,
Ответ
: W=6,16∙10 -13 Дж.
Пример 12.7.
Плоскому конденсатору с площадью обкладокSи расстоянием между ними ℓ сообщён зарядq, после чего конденсатор отключён от источника напряжения. Определите силу притяженияFмежду обкладками конденсатора, если диэлектрическая проницаемость среды между обкладками равна ε.
Дано
:
.
Найти:
F.
Решение
.
Заряд обкладок конденсатора после отключения от источника напряжения не меняется, т.е. q=const. Предположим, что под действием силы притяжения F расстояние между обкладками конденсатора изменилось на d
ℓ
. Тогда сила F совершает работу
Согласно закону сохранения энергии, эта работа равна убыли энергии конденсатора, т.е.
. (3)
Подставив в формулу для энергии заряженного конденсатора выражение для ёмкости плоского конденсатора , получим
(4)
Ответ:
Пример 12.7.
Плоский конденсатор площадью обкладокSи расстоянием между ними ℓ подключен к источнику постоянного напряженияU. Определите силу притяженияFмежду обкладками конденсатора, если диэлектрическая проницаемость среды между обкладками равна ε.
Дано
:
.
Найти:
F.
Решение
.
Согласно условию задачи, на обкладках конденсатора поддерживается постоянное напряжение, т.е. U=const. Предположим, что под действием силы притяжения F расстояние между обкладками конденсатора изменилось на dℓ. Тогда сила F совершает работу
Согласно закону сохранения энергии, эта работа в данном случае идёт на увеличение энергии конденсатора (сравните с предыдущей задачей), т.е.
откуда, исходя из выражений (1) и (2), получим
(3)
Подставив в формулу для энергии конденсатора выражение для ёмкости плоского конденсатора , получим
(4)
Подставив в формулу (3) значение энергии (4) и выполнив дифференцирование, найдём искомую силу притяжения между обкладками конденсатора
.
где знак «-» указывает на то, что сила F является силой притяжения.
Ответ
:
Содержание:
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
Электрическая емкость конденсатора
Дальнейшие опыты с распределением электричества по поверхности наэлектризованного проводника, проводимые Кулоном и другими естествоиспытателями, позволили установить, что равномерное распределение электричества имеет место только на правильной шаровой поверхности. В общем случае заряд неравномерен и зависит от формы проводника, будучи больше в местах большей кривизны. Отношение количества электричества на части поверхности проводника к величине этой поверхности назвали плотностью (толщиной) электрического слоя. Экспериментально было установлено, что электрическая плотность и электрическая сила особенно велики в местах поверхности, имеющих наибольшую кривизну, особенно на остриях.
Интересный материал для ознакомления: что такое вариасторы.
Величину, характеризующую зависимость потенциала наэлектризованного проводника от его размеров, формы и окружающей среды, называют электроемкостью проводника и обозначают буквой С. Электроемкость проводника измеряется количеством электричества, необходимым для повышения потенциала этого проводника на единицу:
Будет интересно➡ Все о законе Ома: простыми словами с примерами для «чайников»
С = q/ϕ.
За единицу электроемкости в системе СИ принимается 1 фарада (1 Ф). Фарадой называется электроемкость проводника, которому для повышения его потенциала на один вольт нужно сообщить один кулон электричества. Электроемкостью, равной 1 Ф, обладал бы шар радиусом 9·10 6 км, что в 23 раза больше расстояния от Земли до Луны. Если проводник соединить с источником электричества определенного потенциала, то проводник получит электрический заряд, зависящий от емкости проводника. Его емкость, а, следовательно, и количество электричества, которым он заряжается, увеличиваются, если приблизить к нему второй проводник, соединенный с землей.
Конструкция, состоящая из двух проводников, разделенных изолятором, с электрическим полем между ними, все силовые линии которого начинаются на одном проводнике, а заканчиваются на другом, была названа электрическим конденсатором. При этом оба проводника называются обкладками, а изолирующая прокладка – диэлектриком. Процесс накопления зарядов на обкладках конденсатора называется его зарядкой. При зарядке на обеих обкладках накапливаются равные по величине и противоположные по знаку заряды.
Поскольку электрическое поле заряженного конденсатора сосредоточено в пространстве между его обкладками, то электроемкость конденсатора не зависит от окружающих тел. Электроемкость конденсатора измеряется отношением количества электричества на одной из обкладок к разности потенциалов между обкладками:
С = q/ U.
1 Ф – электроемкость такого конденсатора, который может быть заряжен количеством электричества, равным 1 Кл, до разности потенциалов между обкладками, равной 1 В. Например, электрическая емкость плоского конденсатора в системе СИ определяется по соотношению:
С =εε 0 S/ d, где ε – диэлектрическая проницаемость материала, находящегося между обкладками конденсатора; ε 0 – диэлектрическая проницаемость вакуума; S – величина площади поверхности пластины (меньшей, если они не равны); d – расстояние между пластинами.
Если обкладки заряженного конденсатора соединить проводником, то заряды будут переходить с одной обкладки на другую и нейтрализуют друг друга. Этот процесс называется разрядкой конденсатора. Каждый конденсатор рассчитан на определенное напряжение. Если напряжение между обкладками станет слишком большим, то разрядка может произойти и непосредственно через диэлектрик (без соединительного проводника), т.е. получится пробой диэлектрика.
Будет интересно➡ Что такое шаговое напряжение и чем оно опасно
Читайте также: Как правильно измерять температуру электронным термометром?
Пробитый конденсатор к дальнейшему употреблению не пригоден. Для получения электроемкости нужной величины конденсаторы соединяют в батарею. На практике встречается как параллельное, так и последовательное соединение конденсаторов.

Строение конденсатора.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Вам это будет интересно Характеристика и схема подключения электросчётчика СО-505
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Назначение
Свойство запасания и отдачи энергии определило широкое применение конденсаторов в современной электронике. Наравне с резисторами и транзисторами они являются основой электротехники. Нет ни одного современного устройства, где они не использовались бы в каком-либо качестве.
Их способность заряжаться и разряжаться совместно с индуктивностью, обладающей теми же свойствами, активно применяются в радио- и телевизионной технике. Колебательный контур из конденсатора и индуктивности — основа передачи и приема сигналов. Изменение емкости конденсатора позволяет менять частоту колебательного контура. Например, радиостанции могут передавать сигнал на своих частотах, а радиоприемники подключаться к этим частотам.
Важной функцией является сглаживание пульсаций переменного тока. Любому электронному устройству, питающемуся от сети переменного тока, для получения постоянного тока хорошего качества необходимы фильтрующие электрические конденсаторы
Активно применяется механизм зарядки и разрядки в фототехнике. Все современные фотоаппараты используют для съемок вспышку, которая реализуется благодаря свойству быстрой разрядки. В данной области невыгодно использовать аккумуляторы, умеющие хорошо запасать энергию, но медленно отдающие ее. А конденсаторы, напротив, моментально отдают всю запасенную энергию, которой достаточно для яркой вспышки.
Возможность генерации конденсаторами импульсов высокой мощности используется в радиолокации и создании лазеров.
Конденсаторы выполняют роль искрогашения контактов в телеграфии и телефонии, а также телемеханике и автоматике, где необходимы переключения высоконагруженных реле.
Регулировка напряжения протяженных линий электропередач осуществляется благодаря использованию компенсационных емкостей.
Современные конденсаторы, благодаря своим возможностям, применяются не только в области радиоэлектроники. Их используют в металлообрабатывающей, горнодобывающей, угольной промышленности.







![]()
Watch this video on YouTube
Электроемкость
Энергия электрического поля
Этим термином характеризуют накопительные способности пассивного элемента. В обозначениях серийных изделий указывают номинальное значение. Так как базовая единица (Ф, фарад) слишком велика, пользуются уменьшительными приставками для обозначения часто применяемых электронных компонентов:
- миллифарад (мФ) – 10-3 Ф;
- нанофарад (нФ) – 10-9 Ф;
- пикофарад (пФ) – 10-12 Ф.
Один фарад соответствует емкости, при которой накопленный единичный заряд (1Кл) создаст разницу потенциалов на пластинах 1 В.
Слободянюк А.И. Физика 10/16.4

Предыдующая страница
16.4 Зарядка конденсатора от источника постоянной ЭДС
Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ε
(Рис. 145). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим R
. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе (
U_C = frac) и резисторе (U_R = IR) равна ЭДС источника (varepsilon = U_C + U_R), что приводит к уравнению
IR = varepsilon — frac) . (1)
В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи (
I = frac), что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени
Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин
Примеры решения задач
ПРИМЕР 1
| Задание | Чему равно расстояние между пластинами плоского конденсатора, если при разности потенциалов В, заряд на пластине конденсатора равен Кл? Площадь пластин , диэлектриком в нем является слюда (). |
| Решение | Емкость конденсатора вычисляется при помощи формулы: Из этого выражения получим расстояние между пластинами: Емкость любого конденсатора определяет формула: где U — разность потенциалов между обкладками конденсатора. Подставим правую часть выражения (1.3) вместо емкости в формулу (1.2), имеем: Вычислим расстояние между обкладками (): |
| Ответ | м |
ПРИМЕР 2
| Задание | Разность потенциалов между пластинами плоского воздушного конденсатора равна В. Площадь пластин равна , расстояние между ними м. Какова энергия конденсатора и чему она будет равна, если пластины раздвинуть до расстояния м. Учтите, что источник напряжения при раздвижении пластин не отключают. |
| Решение | Сделаем рисунок. Энергию электрического поля конденсатора можно найти при помощи выражения: Так как конденсатор плоский, то его электрическую емкость можно вычислить как: |
Рассмотрим теперь энергию, требуемую на то, чтоб зарядить конденсатор. Если заряд Q
был снят с одной обкладки конденсатора и перенесен на другую, то между обкладками возникает разность потенциалов, равная
где С
— емкость конденсатора. Сколько работы затрачено на зарядку конденсатора? Поступая точно так же, как мы поступали с шаром, вообразим, что конденсатор уже заряжен переносом заряда с одной обкладки на другую маленькими порциями
dQ.
Работа, требуемая для переноса заряда
dQ,
равна
Взяв V
из (8.8), напишем
Или, интегрируя от Q = 0
до конечного заряда
Q,
получаем
Эту энергию можно также записать в виде
Вспоминая, что емкость проводящей сферы (по отношению к бесконечности) равна
мы немедленно получим из уравнения (8.9) энергию заряженной сферы
Это выражение, конечно, относится также и к энергии тонкого сферического слоя
с полным зарядом
однородно заряженного
шара [уравнение (8.7)].
Посмотрим, как применяется понятие электростатической энергии. Рассмотрим два вопроса. Какова сила, действующая между обкладками конденсатора? Какой вращательный (крутящий) момент вокруг некоторой оси испытывает заряженный проводник в присутствии другого проводника с противоположным зарядом? На такие вопросы легко ответить, пользуясь нашим выражением (8.9) для электростатической энергии конденсатора и принципом виртуальной работы (см. вып. 1, гл. 4, 13 и 14).
Применим этот метод для определения силы, действующей между двумя обкладками плоского конденсатора. Если мы представим, что промежуток между пластинами расширился на небольшую величину Δz, то тогда механическая работа, производимая извне для того, чтобы раздвинуть обкладки, была бы равна
где F
— сила, действующая между обкладками. Эта работа обязана быть равной изменению электростатической энергии конденсатора, если только заряд конденсатора не изменился.
Согласно уравнению (8.9), энергия конденсатора первоначально была равна
Изменение в энергии (если мы не допускаем изменения величины заряда) тогда равно
Приравнивая (8.12) и (8.13), получаем
что может также быть записано в виде
Ясно, эта сила здесь возникает от притяжения зарядов на обкладках; мы видим, однако,что заботиться о том, как там они распределены, нам нечего; единственное, что нам нужно,— это учесть емкость С.
Легко понять, как обобщить эту идею на проводники произвольной формы и на прочие составляющие силы. Заменим в уравнении (8.14) F
той составляющей, которая нас интересует, а
Δz
— малым смещением в соответствующем направлении. Или если у нас есть электрод, насаженный на какую-то ось, и мы хотим знать вращательный момент τ, то запишем виртуальную работу в виде
где Δθ — небольшой угловой поворот. Конечно, теперь Δ(1/С) должно быть изменением 1/С, отвечающим повороту на Δθ. Таким способом мы можем определить вращательный момент, действующий на подвижные пластины переменного конденсатора, показанного на фиг. 8.3.
Вернемся к частному случаю плоского конденсатора; мы можем взять формулу для емкости, выведенную в гл. 6:
где А
— площадь каждой обкладки. Если промежуток увеличится на
Δz,
то
Из (8.14) тогда следует, что сила притяжения между двумя обкладками равна
Взглянем на уравнение (8.17) повнимательнее и подумаем, нельзя ли сказать, как возникает эта сила. Если заряд на одной из обкладок мы запишем в виде
то (8.17) можно будет переписать так:
поскольку поле между пластинами равно
Можно было сразу догадаться, что сила, действующая на одну из пластин, будет равна заряду Q
этой пластины, умноженному на поле, действующее на заряд. Но что удивляет, так это множитель 1 / 2 . Дело в том, что
Е 0
—это не то поле,
котороедействует на
заряды. Если вообразить, что заряд на поверхности пластины занимает какой-то тонкий слой (фиг. 8.4), то поле будет меняться от нуля на внутренней границе слоя до
Е 0
в пространстве снаружи пластин. Среднее поле, действующее на поверхностные заряды, равно
E 0 /2.
Вот отчего в (8.18) стоит множитель 1 / 2 .
Вы должны обратить внимание на то, что, рассчитывая виртуальную работу, мы предположили, что заряд конденсатора постоянен, что конденсатор не был электрически связан с другими предметами и полный заряд не мог изменяться.
А теперь пусть мы предположили, что при виртуальных перемещениях конденсатор поддерживается при постоянной разности потенциалов. Тогда мы должны были бы взять
и вместо (8.15) мы бы имели
что приводит к силе, равной по величине той, что была получена в уравнении (8.15) (так как V=
Q/C),
но с противоположным знаком!
Конечно, сила, действующая между пластинами конденсатора, не меняет свой знак, когда мы отсоединяем конденсатор от источника электричества. Кроме того, мы знаем, что две пластины с разноименными электрическими зарядами должны притягиваться. Принцип виртуальной работы во втором случае был применен неправильно, мы не приняли во внимание виртуальную работу, производимую источником, заряжающим конденсатор. Это значит, что для того, чтобы удержать потенциал при постоянном значении V, когда меняется емкость, источник электричества должен снабдить конденсатор зарядом VΔC
.
Но этот заряд поступает при потенциале
V,
так что работа, выполняемая электрической системой, удерживающей заряд постоянным, равна V 2 ΔC. Механическая работа
FΔzплюс
эта электрическая работа
V2ΔC
вместе приводят к изменению полной энергии конденсатора на 1
/ 2V2ΔC.
Поэтому на механическую работу, как и прежде, приходится
FΔz=
— 1 / 2 V 2 ΔC.
Обкладки конденсатора, заряженные разноимённо, притягиваются друг к другу.
Механические силы, действующие на макроскопические заряженные тела, называют
пондеромоторными.
Рассчитаем пондеромоторные силы, действующие на обкладки плоского конденсатора. При этом возможны два варианта:
- Конденсатор заряжен и отключён от заряженной батареи
(в этом случае количество зарядов на пластинах остаётся постоянным
q=const).
При удалении одной обкладки конденсатора от другой совершается работа
за счёт которой увеличивается потенциальная энергия системы:
При этом dA = dW . Приравнивая правые части этих выражений, получаем
(12.67)
В данном случае при дифференцировании расстояние между пластинами обозначилось х.
- Конденсатор заряжен, но не отключён от батареи
(в этом случае при перемещении одной из пластин конденсатора будет сохраняться постоянным напряжение (
U=const
). В этом случае при удалении одной пластины от другой потенциальная энергия поля конденсатора уменьшается, так как происходит «утечка» зарядов с пластин, поэтому
Но , тогда
Полученное выражение совпадает с формулой . Оно может быть представлено и в другом виде, если вместо зарядаq ввести поверхностную плотность:
(12.68)
Поле однородно. Напряжённость поля конденсатора равна , где х – расстояние между пластинами. Подставив в формулу U 2 =E 2 x 2 , получим, что сила притяжения пластин плоского конденсатора
(12.69)
Эти силы действуют не только на пластины. Так как пластины, в свою очередь, давят на диэлектрик, помещённый между ними, и деформируют его, то в диэлектрике возникает давление
(S — площадь каждой пластины).
Давление, возникающее в диэлектрике, равно
(12.70)
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора
устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную . Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.