Электромагнитная индукция ℹ️ определение физического явления, формулы, единицы измерения, значение закона Фарадея, применение правила Ленца к направлению потока вектора
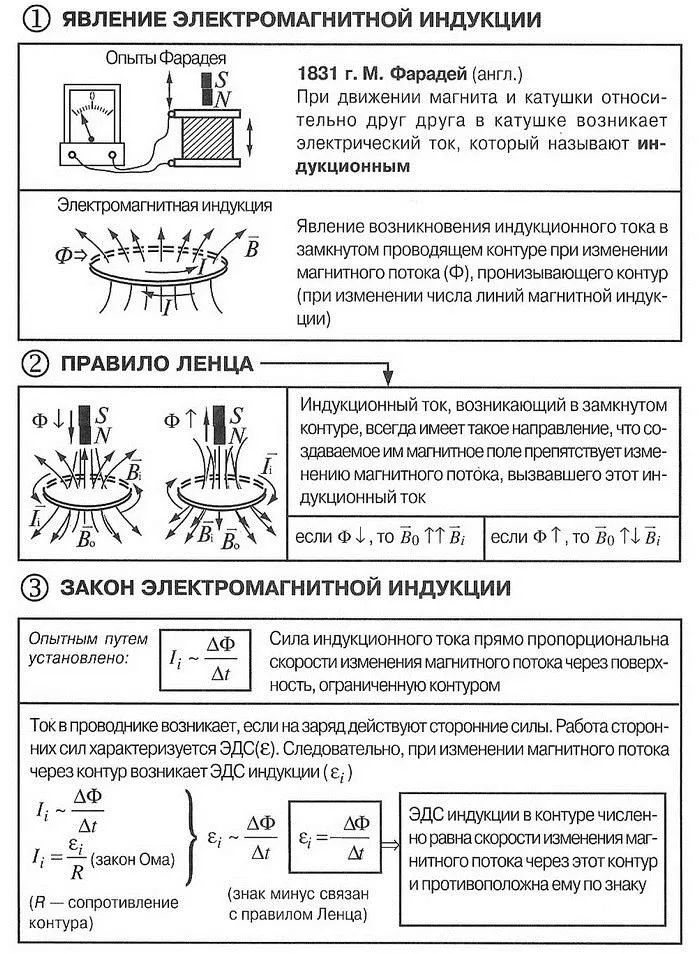
Явление электромагнитной индукции
При изменении тока происходит образование магнитного поля. Это явление, в свою очередь, влияет на движение электронов.
Если рассматривать одиночный провод, расположенный прямо, то он будет создавать поле, направление силовых линий которого идёт по кругу в перпендикулярной ему плоскости.
Если в магнитном поле происходят изменения, то это увеличивает или ослабляет силу тока, который проходит по проводнику. Направление изменения зависит от того, как меняется поле. Это явление позволяет преобразовывать электрическую энергию в механическую или наоборот.

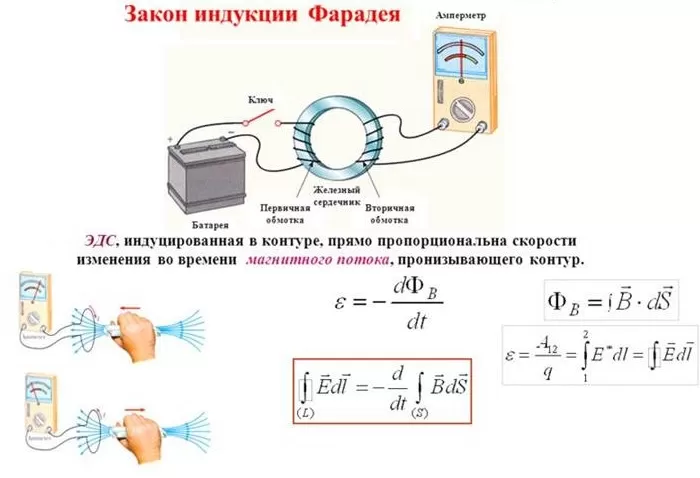
Учёный, которому принадлежит заслуга открытия взаимодействия электрического и магнитного полей — Майкл Фарадей.
Были проведены опыты, которые показали, что изменение магнитного поля способно порождать движение электронов. Это явление впоследствии назвали индукционным током.
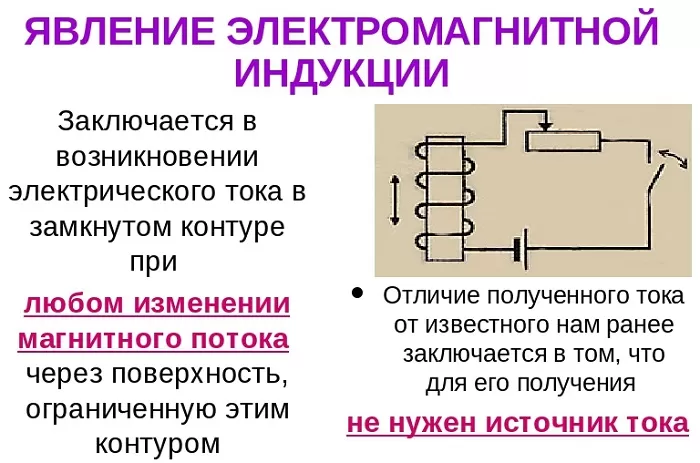
Опыты, выполненные этим учёным, выглядят следующим образом:
-
Фарадей сделал катушку с полой серединой. Её концы соединил с гальванометром. Взял в руки магнит и поместил его внутрь катушки. Если его вдвигать или выдвигать, то на гальванометре отклоняется стрелка, доказывая наличие тока. Чем быстрее выполняемое движение, тем выше его сила. Аналогичный эффект будет достигнут, если магнит будет неподвижен, но будет перемещаться соленоид.
-
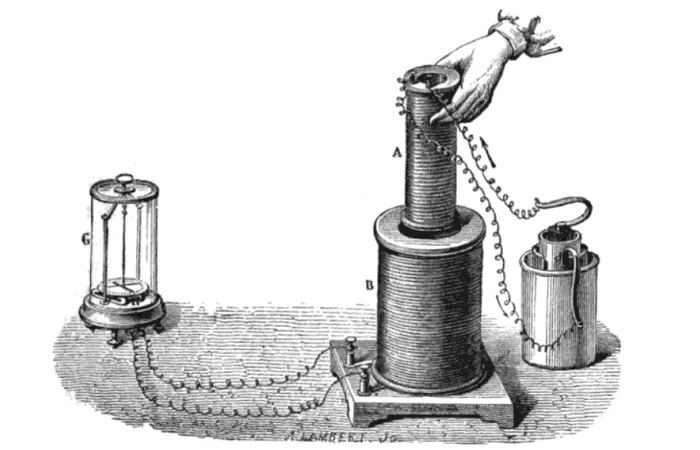
В следующем опыте были использованы две катушки. Большая подключена к гальванометру, а вторая — к источнику. Одна из катушек была настолько узкой, чтоб могла проходить внутрь второй. Если её поместить туда и несколько раз включить и выключить ток, то на гальванометре стрелка отклонится, показывая наличие тока.
-
Если взять два соленоида под током и один из них подвигать рядом с другим, то в них также возникнет движение электронов.
При проведении таких опытов более быстрое движение создаёт более сильное движение электронов.
Одновременно с Фарадеем аналогичные исследования осуществил Джозеф Генри, однако опубликовал свои результаты позже.
Объяснение явления
Движение носителей заряда — электронов происходит в том случае, когда на них действует электродвижущая сила, создаваемая разностью потенциалов.
Возникновение тока под действием изменения магнитного поля происходит из-за того, что оно создаёт такую силу, которая носит название ЭДС индукции. Хотя явление индуктивности было обнаружено Фарадеем, он не дал ему теоретического объяснения.
Теория электромагнитного поля в физике была создана Максвеллом в 1861 году. Этому явлению присущи такие черты:
-
источником движения электронов является переменное магнитное поле;
-
его наличие можно обнаружить по производимому воздействию на электрические заряды;
-
это поле не является потенциальным;
-
силовые линии поля представляют собой замкнутые кривые.
Работа магнитного поля выражается в создании электродвижущей силы для электронов.
Закон электромагнитной индукции Фарадея
Основной характеристикой магнитного поля является магнитный поток. Зрительно его можно представить, как силовые линии, пронизывающие перпендикулярную плоскую фигуру, ограниченную замкнутой линией. Эти линии выражают вектор магнитной индукции.
Произведение модуля этой величины на площадь для равномерного и однородного магнитного поля равно потоку поля через рассматриваемый контур.
При рассмотрении сложного поля, фигуру разбивают на небольшие участки, в которых поле равномерно и суммируют значения для каждого из них. Для вычисления в таких случаях используются методы дифференциального и интегрального исчисления.
Электромагнитная индукция измеряется в Тесла (Тл). Эта единица получила своё название в честь великого учёного-физика.
Закон Фарадея количественно описывает влияние магнитного поля на движение электронов. Он утверждает следующее: скорость изменения потока электромагнитного поля равна порождаемой им электродвижущей силе, воздействующей на электроны и создающей ток.
Нужно заметить, что когда магнитное поле порождается изменением силы тока, то возникающая электродвижущая сила воздействует на него противоположным образом. Это можно прояснить на таком примере.
Если рассматривается провод, и в нём увеличивается сила тока, то это создаёт магнитное поле. Оно, в свою очередь, создаёт ЭДС, которая препятствует увеличению.
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно Рис. 9. Движение проводника в магнитном поле Возьмём внутри стержня положительный свободный заряд Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!). Сила Лоренца (Длину стержня мы также считаем равной Таким образом, стержень Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце Теперь предположим, что рельсы и перемычка Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это. Магнитный поток через контур увеличивается. Приращение магнитного потока равно: Скорость изменения магнитного потока положительна и равна ЭДС индукции: Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые. Поделиться страницей
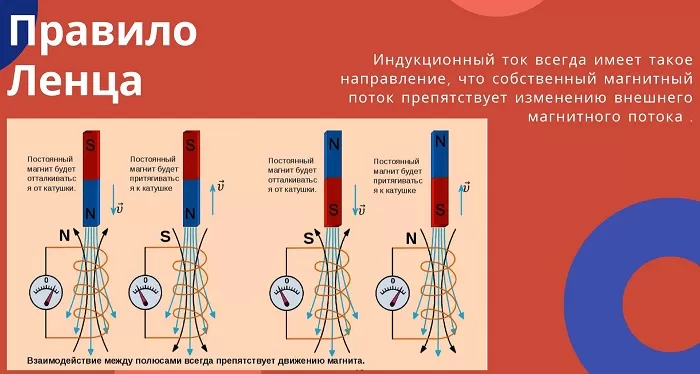
Это правило даёт возможность правильно определить направление индукционного тока в различных ситуациях. Оно формулируется следующим образом: направление тока, порождённого индукцией, создаёт такое изменение магнитного потока, препятствующее изменению внешнего поля, благодаря которому оно возникло.
Это можно пояснить на следующем примере. Будет рассмотрена ситуация, когда внешнее магнитное поле со временем будет возрастать, а его силовые линии направлены вверх.
Это произойдёт, например, в той ситуации, когда снизу к контуру, расположенному горизонтально, будут приближать магнит так, чтобы его северный полюс был обращён вверх. В этом случае магнитный поток будет увеличиваться, создавая электродвижущую силу.
В контуре будет создан индукционный ток. Он будет таким, чтобы магнитные силовые линии были противоположными по отношению к тем, которые характеризуют первоначальное. Теперь можно определить направление индукционного тока в контуре.
На этом примере можно увидеть, как с помощью правила Ленца можно определить направление магнитного поля и индукционного тока.
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил? Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток. Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом. Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора Рис. 7. Вихревое электрическое поле при увеличении магнитного поля Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8). Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток. Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток. 1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных. Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура . Пусть, например, контур является кольцом радиуса Следовательно, для ЭДС индукции получаем:
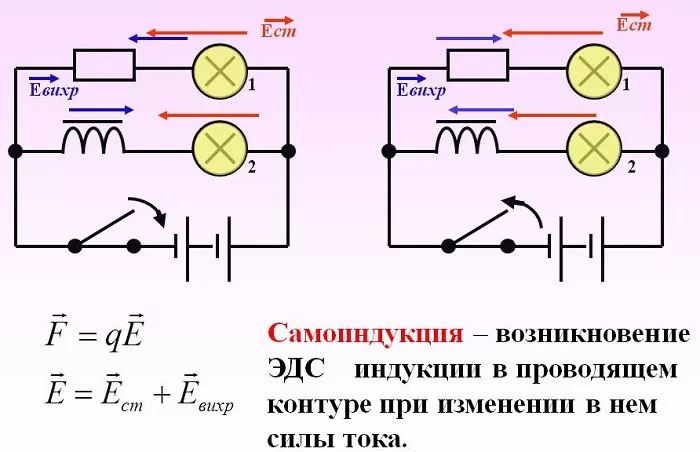
В этом случае рассматривается ситуация, когда изменение движения электронов порождает ЭДС, вызывающий индукционный ток в этом же проводнике.
Взяв за основу правило Ленца, можно утверждать, что он имеет направление, противоположное первоначальному изменению.
Самоиндукция похожа на явление инерции. Тяжёлое тело невозможно остановить мгновенно. Также нельзя изменить силу тока за один миг до нужной величины из-за наличия явления самоиндукции.
Это свойство можно продемонстрировать следующим опытом. Нужно сделать две электрических цепи. В одной из них имеется источник и лампочка. Другая сделана аналогичным образом, но различие состоит в том, что в цепь добавлена катушка.
В первой цепи после включения лампочка загорается сразу. Во второй, учитывая наличие индуктивного элемента, это происходит с заметным опозданием.
После размыкания свет в первой лампочке отключается практически мгновенно, а во второй это происходит замедленно. Важно отметить, что в процессе выключения индукционный ток может превысить первоначальный. Поскольку в этой ситуации он направлен также, как и рабочий, то сила тока может возрасти. В некоторых цепях это может вызвать перегорание лампочки.
Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной. Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор. Магнитный поток через контур считается положительным ЭДС индукции считается положительной Итак, пусть контур находится в магнитном поле Рис. 5. Магнитный поток возрастает Стало быть, в данном случае имеем А именно, предположим теперь, что магнитный поток убывает Рис. 6. Магнитный поток возрастает Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
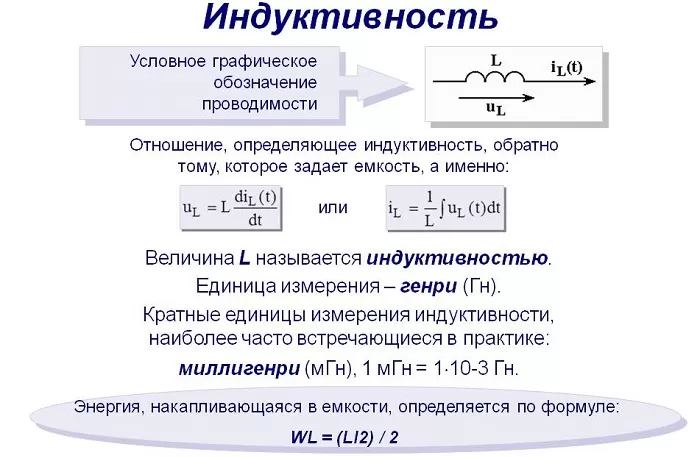
Проводник, через который проходит изменяющийся ток, способен накапливать энергию путём использования магнитного поля. У прямолинейного отрезка провода эта способность имеет незначительную величину.
Однако, если речь идёт о катушке, то её величина гораздо сильнее. Эта характеристика называется индуктивностью. Она обозначается как «L» и играет важную роль при определении различных характеристик электромагнитного поля.
Магнитный поток в определённом контуре можно выразить посредством формулы Ф = L* I, а электродвижущую силу в виде E = L* (dI/dt).
Ток, проходящий через контур, способен создать электромагнитное поле, причём оно будет тем сильнее, чем быстрее будут происходить его изменения.
На практике для увеличения индуктивности катушки используют вставленные внутрь стержни из ферромагнетика.
Электрический ток создаёт магнитное поле. При этом он затрачивает определённую энергию. Её величина равна той работе, которая была затрачена на создание поля. Она вычисляется по следующей формуле:
Здесь использовались такие обозначения:
W – энергия магнитного поля;
L – индуктивность;
I – сила тока.
Если магнитное поле по какой-то причине пропадёт, то его энергия выделится в той или иной форме.
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности): Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб). Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции: Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь. В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0. Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его). В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность. Слышали ли вы когда-нибудь такое выражение: “напряженность между ними все росла и росла”. То есть по сути напряженность – это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой где H – напряженность магнитного поля, Ампер/метр B – плотность магнитного потока, Тесла μ0 – магнитная постоянная = 4π × 10-7 Генри/метр или если написать по человечески 1,2566 × 10-6 Генри/метр. PS. Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так. где μ – это относительная магнитная проницаемость. У разных веществ она разная Итак, имеем какой-либо проводник, по которому течет электрический ток. Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой где H – напряженность магнитного поля, Ампер/метр I – сила тока, текущая через проводник, Ампер r – расстояние до точки, в которой измеряется напряженность, метр
Это явление активно применяется в различных сферах жизни человеческого общества.
Далее будут приведены несколько наиболее известных примеров:
радиовещание невозможно без использования явления электромагнитной индукции;
в медицине магнитотерапия является одним из эффективных методов лечения;
при фундаментальных исследованиях для разгона элементарных частиц применяются синхрофазотроны, работа которых основана на явлении индуктивности;
счётчики электричества, применяемые в быту для его учёта, используют рассматриваемое явление;
для того, чтобы передавать произведённую электростанциями электрическую энергию на большие расстояния, применяются трансформаторы, работа которых построена на использовании электромагнитной индукции;
в металлургии для плавки металла применяются индукционные печи.
Использование этого явления очень широко распространено. Приведённые примеры являются только частью различных вариантов использования.
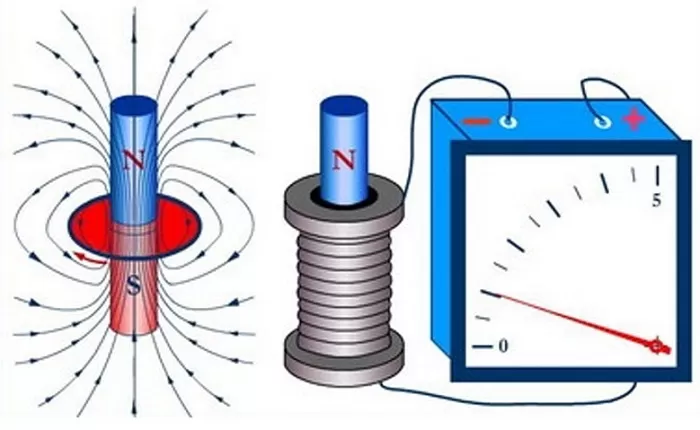
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле. Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу. Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии – они замкнуты и непрерывны. В магните это будет выглядеть примерно так. Если приблизить два разноименных полюса, то произойдет притягивание магнитов Если же приблизить одноименными полюсами, то произойдет их отталкивание Итак, ниже важные свойства магнитных силовых линий. Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком. Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке “а” или на рисунке “б”? Видим, что на рисунке “а” мало силовых магнитных линий, а на рисунке “б” их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке “б” больше, чем на рисунке “а”. В физике формула магнитного потока записывается как где Ф – магнитный поток, Вебер В – плотность магнитного потока, Тесла а – угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах S – площадь, через которую проходит магнитный поток, м2 Что же такое 1 Вебер? Один вебер – это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м2 расположенной перпендикулярно направлению магнитного поля.
Для того чтобы кратко освежить в памяти формулы, относящиеся к магнитной индукции, далее приводится перечень наиболее важных из них.
Открытие законов, которые описывают поведение электромагнитного поля, является одним из важнейших достижений науки за всю историю. В современной жизни использование этого явления происходит практически во всех областях жизни общества.
Понравилась статья? Поделитесь ей А какая Ваша оценка этой статьи? 12345 Чтобы сюда попасть — пройдите тест Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила? Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая. 1. Магнит приближаем к контуру, северный полюс направлен на контур. Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий. Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет . Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1 Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии. Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток. Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания . Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения. Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две: Перейдем к рассмотрению этих случаев подробнее. При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила. Пример 2 На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью. Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен: FЛ=eυ→B. Работа силы FЛ на пути l равна: A=FЛ·l=eυBl. По определению ЭДС: δинд=Ae=υBl. Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt. Следовательно, δинд=∆Φ∆t. Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея. При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло: ∆Q=RIинд2∆t=υ2B2l2R∆t Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→. Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле: Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
. Рельсы находятся в вертикальном однородном магнитном поле 
. По рельсам движется тонкий проводящий стержень 
со скоростью 


. Вследствие движения этого заряда вместе со стержнем со скоростью 
на заряд будет действовать сила Лоренца:

играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда 
от точки 
к точке 
наша сторонняя сила совершит работу:

.) Стало быть, ЭДС индукции в стержне окажется равной: 
(7)
аналогичен источнику тока с положительной клеммой 
и отрицательной клеммой 
. Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке 
, отрицательные — к точке 
.
и отрицательных зарядов на торце 
будет возрастать кулоновская сила, с которой положительный свободный заряд 
отталкивается от 
и притягивается к 
— и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7). 
являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении 
(от «плюса источника» 
к «минусу» N). Предположим, что сопротивление стержня равно 
(это аналог внутреннего сопротивления источника тока), а сопротивление участка 
равно 
(сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
За время 
наш стержень 
проходит путь 
и занимает положение 
(рис. 9). Площадь контура возрастает на величину площади прямоугольника 
:



, то его магнитное поле направлено противоположно внешнему полю 
и, стало быть, препятствует возрастанию магнитного потока через контур. Правило Ленца
Как известно, если смотреть со стороны создаваемого поля, то он будет направлен по часовой стрелке. То есть, если смотреть сверху, направление будет против неё.Вихревое электрическое поле

. Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
, (рис. 7). 

2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
и пронизывается однородным переменным магнитным полем. Тогда напряжённость 
вихревого электрического поля одинакова во всех точках кольца. Работа 
силы 
, с которой вихревое поле действует на заряд 
, равна: 

Самоиндукция

Закон Фарадея + Правило Ленца = Снятие модуля

.
, если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
. Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: 


. Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
. По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, 

(6)Индуктивность
Энергия магнитного поля
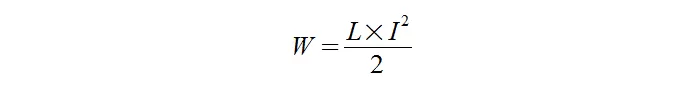
Магнитный поток



Напряженность магнитного поля
Формула напряженности






Напряженность магнитного поля проводника с током




Применение электромагнитной индукции

Магнитные линии и магнитный поток














Все формулы по теме «Электромагнитная индукция»

2.4 из 5Доска почета
Взаимодействие магнита с контуром
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Перемещение контура или его частей в неизменном магнитном поле