Отбросьте в сторону все ваши умные книги — мы займемся практикой.

Вы когда-либо пробовали разобраться, что такое полное электрическое сопротивление, которое еще называют импедансом? Если раньше вы уже успели окунуться в эту тему, то скорее всего, уже нахватались жаргонных словечек, таких как «фазовый вектор», «соотношения фаз» и даже «реактивное сопротивление». Какого черта, что все это значит?

Не все из нас по образованию инженеры-электрики. Некоторые в свободное время просто возятся с электроникой, но никогда не касаются строгих математических обоснований, которые вы изучали в университете. Однако это не означает, что отсутствие понимания, что такое полное электрическое сопротивление должно стать препятствием. Если вы планируете работать с электронными устройствами переменного тока, то вам нужно знать, что такое полное сопротивление, и как оно влияет на вашу электрическую цепь.

Давайте выясним это!

Не совсем яблочко от яблоньки

Лучший способ понять, что же такое полное электрическое сопротивление – это сравнить его с чем-то уже вам известным, скажем – «простым» сопротивлением. Так мы сможем дать исчерпывающее определение полного электрического сопротивления одной фразой:

Полное электрическое сопротивление – это вид сопротивления, зависящее от частоты.

Вот и всё. Сейчас вы можете остановиться и записать еще одно слово в ваш словарь инженера-электрика. Просто и понятно: полное электрическое сопротивление – вид сопротивления, которое зависит от рабочей частоты электрической цепи. Но, разумеется, это еще не всё.

Резисторы выполняют в цепи постоянного тока чрезвычайно простую работу. Они оказывают сопротивление току, протекающему через какой-либо металл, например медь. Вы добавляете резистор на 220 кОм в цепь постоянного тока, и получаете определенное уменьшение тока, который втекает в резистор с одной стороны, и вытекает из него с другой стороны. Резисторы, подобно другим чисто омическим компонентам электрической цепи, не думают о том, какую же частоту выдает источник тока. Они просто делают то, что должны делать – оказывают некое постоянное сопротивление току.

Но что произойдет, если вы начнете работать с электроникой с питанием от источника переменного тока? Источник переменного тока не просто дает 5 В для питания вашей схемы. Кроме нового источника тока вы получили новые переменные, с которыми необходимо считаться. Например, сюда входит заранее известная частота переменного тока в сети питания. В Соединенных Штатах Америки частота тока в электрической сети составляет 60 колебаний в секунду (60 Гц). За океаном, в Европе, частота тока в сети 50 Гц.

В отличие от постоянного тока (DC), график которого представляет собой

прямую линию, переменный ток (АС) колеблется с определенной частотой.

В итоге получается следующее: в электронных устройствах, использующих переменный ток, необходимы не только активные компоненты, такие как резисторы, задачей которых является оказание сопротивления электрическому току, также нужны компоненты, которые могут реагироватьна изменения тока и частоты, например конденсаторы и катушки индуктивности. В противном случае электрическая схема не будет работать так, как задумывалось. Зная все это уже можно посчитать полное сопротивление, которое является старшим братом активного сопротивления. Полное электрическое сопротивление включает в себя и активное, и реактивное сопротивления. Это можно записать в виде выражения:

Полное сопротивление =
активное сопротивление + реактивное сопротивление

Но что такое реактивное сопротивление?

Реактивное сопротивление бывает двух видов в зависимости от используемого реактивного компонента. Сюда входит:

Индуктивное реактивное сопротивление

Оно встречается в цепях, где есть своего рода электромагниты, влияющие на магнитное поле электрической цепи. Еще их называют катушками индуктивности. Катушки индуктивности имеют низкое полное электрическое сопротивление на низких частотах и высокое полное электрическое сопротивление на высоких частотах.

Разные катушки индуктивности. Обратите внимание на общность

конструкции – медный провод намотан на магнит, образуя катушку.

Емкостное реактивное сопротивление

Оно встречается там, где электрическое поле между двумя проводящими поверхностями вызывает накопление заряда. Такие устройства еще называют конденсаторами. Конденсаторы имеют высокое полное электрическое сопротивления на низких частотах и низкое полное сопротивление на высоких частотах.

Конденсаторы встречаются всех форм и размеров.

Соберем электрическую цепь переменного тока из резисторов, катушек индуктивности и конденсаторов. Теперь вы сможете не только оказывать сопротивление электрическому току, но и накапливать и высвобождать энергию. Если резисторы сохраняют постоянное сопротивление вне зависимости от изменяющихся условий, то сопротивление катушек индуктивности и конденсаторов изменяется в зависимости от частоты проходящего через них электрического сигнала. Когда конденсаторы и катушки индуктивности вместе оказывают сопротивление и накапливают/высвобождают энергию, тогда и говорят о полном электрическом сопротивлении.

Зависимость электропроводимости

R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.

Электрические величины

К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.

Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).

Геометрические параметры и тип вещества

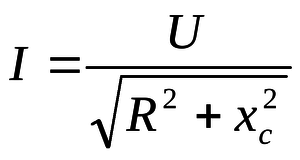
Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.

Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.

Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:

1. Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
2. Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.

П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.

Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:

1. Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
2. Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.

Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:

1. Визуально определить геометрическую фигуру при разрезе П.
2. Найти в справочнике формулу S.
3. Произвести измерения при помощи ШЦ необходимых величин.
4. Подставить в формулу и вычислить S.

Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.

Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.

Температура проводника

Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.

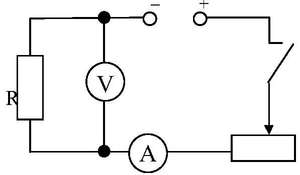
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.

В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:

• для металлов а > 0;
• для электролитов a < 0.

Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.

В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.

Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.

Расчет эквивалентного сопротивления элементов цепи

Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.

Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:

I=U/Z, где Z – общий импеданс цепи.

Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.

Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.

Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:

Z2=1/(1/R2+(1/ XL – 1/ XC)2).

Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.

Как измерить полное электрическое сопротивление

Соединим все детали вместе в простую электрическую цепь. Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.

Простая цепь постоянного тока с резистором

на 100 Ом для ограничения силы тока.

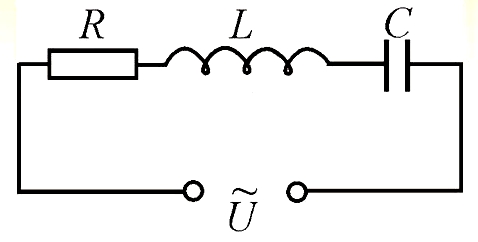
Что произойдет, если мы добавим в электрическую цепь источник питания переменного тока, катушку индуктивности и конденсатор? Теперь в цепи есть два дополнительных компонента, каждый из которых по своему оказывает сопротивление электрическому току. Как и резистор, они оба препятствуют прохождению электрического тока, при этом также воздействуют на ток. Если суммировать активное сопротивление резистора и активное и реактивное сопротивления конденсатора и катушки индуктивности, то получится полное электрическое сопротивление или импеданс.

В цепи переменного тока последовательно соединены резистор, катушка индуктивности и конденсатор

Постойте! Чтобы рассчитать полное электрическое сопротивления недостаточно просто сложить активные и реактивные сопротивления. Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.

Понятие тока и напряжения

Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.

Вам это будет интересно  Понятие и нахождение электрической мощности по формулам

В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.

Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.

Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.

Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.

При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.

Полное сопротивление цепей переменного тока

При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:

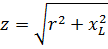
Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то

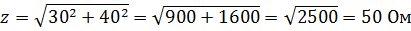
т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.

Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению. Ошибка весьма невелика.

Например, если r = 1 Ом и xL = 10 Ом, то

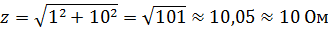
Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.

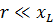
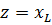
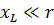
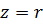
При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости

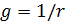
и реактивной проводимости

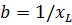
Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:

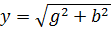
А полное сопротивление цепи является величиной, обратной у,

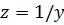
Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:

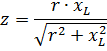
Эта формула напоминает известную формулу

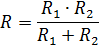
но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.

Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.

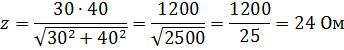
При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %

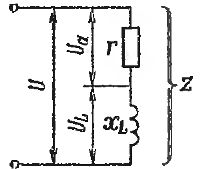
Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением

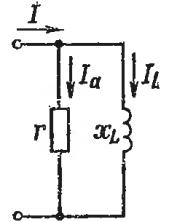
Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением

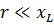
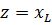
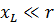
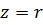
Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:

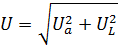
При параллельном соединении (рис. 2) складываются токи:

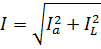
Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.

При любой цепи переменного тока закон Ома можно писать в следующем виде:

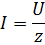
где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.

Коэффициент мощности cosφ для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:

Читайте также:  Опыт картина магнитного поля проводника с током

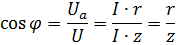
При параллельном соединении получим:

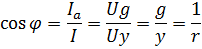
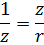
Вывод основных расчетных формул для последовательной цепи переменного тока, имеющей активное и индуктивное сопротивления, можно сделать следующим образом.

Проще всего построить векторную диаграмму для последовательной цепи (рис. 3).

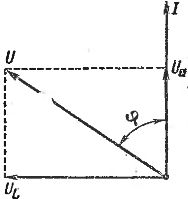
Рис. 3. Векторная диаграмма для последовательной цепи с активным и индуктивным сопротивлением

На этой диаграмме показаны вектор тока I, вектор напряжения UA на активном участке, совпадающий по направлению с вектором I, и вектор напряжения UL на индуктивном сопротивлении. Это напряжение опережает ток на 90° (напомним, что векторы надо считать вращающимися против часовой стрелки). Полное напряжение U представляет собой суммарный вектор, т. е. диагональ прямоугольника со сторонами UA и UL. Иначе говоря, U есть гипотенуза, а UA и UL — катеты прямоугольного треугольника. Отсюда следует, что

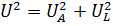
Т. е. что напряжения на активном и реактивном участках складываются геометрически.

Разделив обе части равенства на I2, найдем формулу для сопротивлений:

Источник

Аналогия с электрическим сопротивлением проводника на примере резистора

От чего зависит сопротивление проводника

Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.

Активное сопротивление

Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.

Важно! Выражение для сопротивления резистора можно записать так: R=U/I.

Резисторы – источники активного сопротивления

Реактивное сопротивление

К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.

Индуктивная нагрузка

Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:

R=U/I=0/I=0.

Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности

Емкостная нагрузка

При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.

Детали, обладающие емкостью

Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.

Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами.

Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.

Емкостная проводимость линий

Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.

Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:

Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.

Расчет полного электрического сопротивления конденсатора

Чтобы найти полное электрическое сопротивление конденсатора, вы можете воспользоваться следующей формулой. В ней Xc – полное электрическое сопротивление, которое необходимо найти. Оно измеряется в Омах. Переменная f – это частота сигнала, проходящего через конденсатор, а C – емкость конденсатора.

Виды источников переменного напряжения

Среди основных источников непостоянного напряжения можно выделить такие компоненты, как:

• Электростанция;
• Генератор непостоянного тока;
• Промышленная и домашняя электросеть.

Главным источником непостоянных токовых сил и напряжения является электростанция или промышленная электросеть. Использование такого тока обосновано тем, что его намного легче передавать на большие расстояния по проводникам и просто преобразовать в постоянный электрический ток. Переменные параметры передаются со станции к трансформаторам, которые преобразуют напряжение непостоянного тока, не являясь его источниками. Генераторы вырабатывают такой ток путем преобразования механической энергии в электрическую.

Генератор переменной силы

Электрический ток. Закон Ома для цепей постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.

Начнём с терминологии.
Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи — физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление — это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.

Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P(Вт) = U(В)×I(А) = I 2 (А)×R(Ом) = U 2 (В)/R(Ом)

Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:

Читайте также:  Правила пользования генератором переменного тока

Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

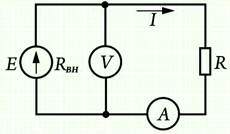
Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр.
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/Rll = 1/R4+1/R5 .
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид:

Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

Источник

Сравнение влияния реактивного сопротивления на активную мощность сети

Из рисунков 1 и 2 видно, что сдвиг фаз на рисунках не одинаков. Вывод — чем больше в полном сопротивлении Z будет влияние XL или XC тем больше будет разница фаз U и I.

Угол сдвига между током и напряжением называется φ .

Реактивная мощность однофазная:

Трехфазная:

Uф, Iф — фазные ток и напряжение

Вывод: реактивная мощность – не выполняет полезного действия.

Она «перегоняется» по сети нагревая кабели и увеличивая потери. На крупных промышленных предприятиях это особо ощутимо в силу наличия электроприводов и других крупных потребителей. Этот вопрос очень актуален для энергосбережения и модернизации производства. Поэтому на пром. предприятиях устанавливаются компенсаторы реактивной мощности. Они могут быть разного типа и кроме компенсации выполнять еще и роль фильтров. С помощью компенсаторов стараются сохранить баланс реактивной мощности для минимизации ее влияния на сеть и подогнать угол φ к нулю.

Для компенсации реактивной мощности необходимо максимально сбалансировать в сети количество (L, C) элементов.

Расчет полного электрического сопротивления катушки индуктивности

Расчёт полного сопротивления цепи под действием переменного тока

Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.

• Физический смысл
• Зависимость электропроводимости
  • Электрические величины
  • Геометрические параметры и тип вещества
  • Температура проводника
• Цепь переменного тока
• Измерение сопротивления

Расчет полного электрического сопротивления цепи

Чтобы выполнить расчет, вам необходимо обратиться за помощью к теореме Пифагора. Как мы уже рассказали выше, в цепях переменного тока действуют и активное, и реактивное сопротивления, вместе образуя полное электрическое сопротивление. Но простое суммирование активного и реактивного сопротивления не имеет смысла. Мы можем объяснить, почему это так, но тогда нам придется рассказать о премудростях фазовых векторов и о правилах работы с ними, а для этого понадобится отдельный блог.

Когда вы сталкиваетесь с расчетом полного электрического сопротивления всей цепи, вам может помочь то, что называется треугольником сопротивлений, который показан на рисунке ниже.

Треугольник сопротивлений упрощает расчет

полного электрического сопротивления цепи.

Наиболее важная часть этого треугольника – его гипотенуза, дает величину полного сопротивления цепи, которое представляет собой квадратный корень из суммы квадратов активного и реактивного сопротивлений. Если вы подставите их в данную формулу, то сможете найти полное сопротивление электрической цепи. В ней Z – это искомое полное электрическое сопротивление цепи, R – полное активное сопротивление, X – полное реактивное сопротивление.