Определение и формулы для расчета и измерения индуктивности: в чем измеряется

Введение

Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.

При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.

Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio

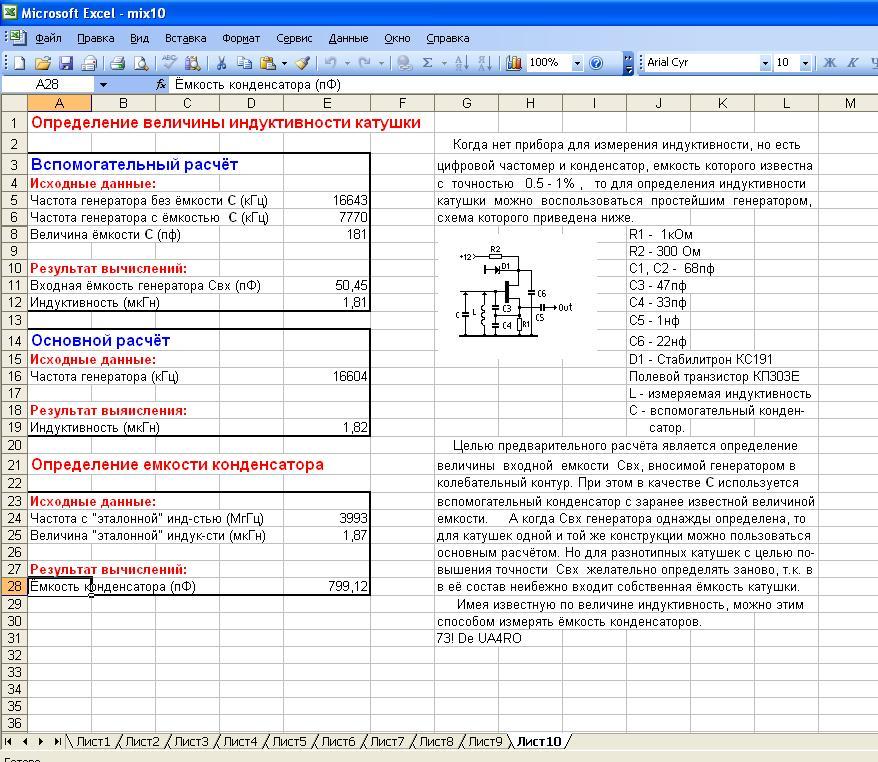
— наведение, побуждение — и обозначают совершенно разные понятия.

Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.

Читайте также:  Как правильно установить трансформаторы тока на шины

Определение индуктивности

В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:

или

Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.

При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:

Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:

То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.

Проведём исследование поведения тока в индуктивности:

Рис. 1. Электрическая схема эксперимента

Рис. 2. Физическая реализация эксперимента

Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.

Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.

Проведём исследование напряжения на катушке индуктивности:

Рис. 4. Электрическая схема эксперимента

Рис. 6. Осциллограмма напряжения на индуктивности (голубая)

Читайте также:  Проектирование внутреннего освещения помещений

В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.

Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) B{displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки является фактически постоянной и (приближённо) равна

B=μNil{displaystyle displaystyle B=mu _{0}Ni/l}

или

B=μni,{displaystyle displaystyle B=mu _{0}ni,}

где μ{displaystyle mu _{0}} − магнитная постоянная, N{displaystyle N} − число витков, i{displaystyle i} − ток, записанный в амперах , l{displaystyle l} − длина катушки в метрах и n{displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{displaystyle B} , умноженному на площадь поперечного сечения S{displaystyle S} и число витков N{displaystyle N}:

Ψ=μN2iSl=μn2iV,{displaystyle displaystyle Psi =mu _{0}N^{2}iS/l=mu _{0}n^{2}iV,}

где V=Sl{displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

Читайте также:  Пример расчета уставок кабельной линии 10 кВ с ответвлениями

L=μN2Sl=μn2V.{displaystyle displaystyle L=mu _{0}N^{2}S/l=mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель μ{displaystyle mu } — относительную магнитную проницаемость сердечника:

L=μμN2Sl=μμn2V.{displaystyle displaystyle L=mu _{0}mu N^{2}S/l=mu _{0}mu n^{2}V.}

В случае, когда μ>>1{displaystyle mu >>1}, можно (следует) под S

понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются:w,Dкаркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

ЗнаяDкаркаса иL, рассчитывают количество витков в катушке, формула имеет вид:

где:

• L – индуктивность, мкГн;
• D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

где:

• l – длина намотки, мм;
• d – диаметр провода, мм.

Измерения диаметра провода проводят линейкой или штангенциркулем.

Расчёт индуктивности прямого провода

Собираясь найтиLкруглого прямого проводника, обращаются к приближённой формуле:

L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,

где:

• μ0 – магнитная постоянная;
• μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
• μi – ОМП проводника;
• l – длина провода;
• r – радиус провода.

Формула справедлива для длинного проводника.

Расчёт однослойной намотки

Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.

Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:

L = D2*n2/45D + 100*l,

где:

• D – диаметр катушки, см;
• l – длина намотанного провода, см;
• n – количество витков.

Формула подходит для вычислений L дросселей без ферритовых сердечников.

Читайте также:  Переменное напряжение и постоянное напряжение отличия

Дроссель с сердечником

При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

Многослойная намотка

Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:

где:

• Dk – общий диаметр (диаметр каркаса и намотки);
• t – толщина слоя;
• l – длина накрученного провода.

Все значения подставляют в мм, величину L – в мкГн.

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками

Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах

Автор статьи: Анатолий Золотков

Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:

Калькулятор резистивно-емкостной цепи

Калькулятор параллельных сопротивлений

Калькулятор параллельных индуктивностей

Калькулятор емкости последовательного соединения конденсаторов

Калькулятор импеданса конденсатора

Калькулятор импеданса катушки индуктивности

Калькулятор взаимной индукции

Калькулятор взаимоиндукции параллельных индуктивностей

Калькулятор взаимной индукции — последовательное соединение индуктивностей

Калькулятор импеданса параллельной RC-цепи

Калькулятор импеданса параллельной LC-цепи

Калькулятор импеданса параллельной RL-цепи

Калькулятор импеданса параллельной RLC-цепи

Калькулятор импеданса последовательной RC-цепи

Калькулятор импеданса последовательной LC-цепи

Калькулятор импеданса последовательной RL-цепи

Калькулятор импеданса последовательной RLC-цепи

Калькулятор аккумуляторных батарей

Калькулятор литий-полимерных аккумуляторов для дронов

Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC)

Калькулятор расчета параметров коаксиальных кабелей

Калькулятор светодиодов. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов

Калькулятор цветовой маркировки резисторов

Калькулятор максимальной дальности действия РЛС

Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов

Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС

Калькулятор радиогоризонта

Калькулятор эффективной площади антенны

Симметричный вибратор

Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации

Калькулятор мощности постоянного тока

Калькулятор мощности переменного тока

Калькулятор пересчета ВА в ватты

Калькулятор мощности трехфазного переменного тока

Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую

Калькулятор коэффициента гармонических искажений

Калькулятор законов Ома и Джоуля — Ленца

Калькулятор времени передачи данных

Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора

Калькуляторы Электротехнические и радиотехнические калькуляторы

Ресчет катушек индуктивности (однослойных, цилиндрических)

Рис. 1. Пример однослойной катушки индуктивности.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников. Расчет однослойных цилиндрических катушек производится по формуле:

где:

• L — индуктивность катушки, мкГн;
• D — диаметр катушки, см;
• I — длина намотки катушки, см;
• n — число витков катушки.

При расчете катушки могут встретиться два случая:

• а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
• б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 1; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода.

Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле:

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле:

где:

• d — диаметр провода, мм,
• l — длина обмотки, мм,
• n — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины, получим:

Диаметр провода:

Если эту катушку наматывать проводом меньшего диаметра, то нужио полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки.

Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки.

Возможно, также придется увеличить и то и другое одновременно, пока не будут получепы необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным пыше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше D половины диаметра то более точные результаты можно получить по формулам:

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Советуем изучить Нормативы потребления электроэнергии на человека без счетчика

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Какие параметры есть у катушки

От того, где будет применяться индуктивный элемент и на какой частоте работать, зависит его исполнение. Имеются общие параметры:

• L – индуктивность;
• R пот – сопротивление потерь;
• Q – добротность;
• свой резонанс и паразитарная ёмкость;
• коэффициенты ТКИ и ТКД.

Расчет трансформатора

Индуктивность (коэффициент самоиндукции) L – это главная электрическая характеристика элемента, которая показывает количество накапливаемой дросселем энергии при передвижении тока. Величина энергии в катушки тем выше, чем больше её индуктивность. Единица измерений L – 1 Гн.

При взаимодействии тока и магнитного поля в обмотке возникают вредные явления. Они способствуют возникновению потерь, которые обозначают R пот. Формула потерь имеет вид:

R пот = rω + rd + rs + re.

Слагаемые формулы – это потери:

• rω – в проводах;
• rd – в диэлектрике;
• rs – в сердечнике;
• re – на вихревые токи.

В результате таких потерь импеданс индуктивного двухполюсника нельзя назвать целиком реактивным.

Добротность двухполюсника определяется по формуле:

Q = ω*L/R пот,

где ω*L = 2π*L – реактивное сопротивление.

При наматывании витков элемента между ними возникает ненужная ёмкость. Из-за этого дроссель превращается в колебательный контур с собственным резонансом.

ТКИ – показатель, описывающий зависимость L от Т0С.

ТКД – показатель, описывающий зависимость добротности от Т0С.

Информация. Изменение основных параметров индуктивного двухполюсника зависит от коэффициентов ТКИ, ТКД, а также от времени и влажности.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

Ce = C : (1 — 4Π2f2LC),

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

Lk = Lp + Lm + Lb,

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного сердечника плотность магнитного потока (или магнитная индукция) B{displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки вдали от её концов (приближённо) равна

B=μNil{displaystyle displaystyle B=mu _{0}Ni/l}

или

B=μni,{displaystyle displaystyle B=mu _{0}ni,}

Читайте также:  Основные соотношения линейных и фазных токов , при соединение элементом трехфазной цепи в звезду

где μ{displaystyle mu _{0}} − магнитная постоянная, N{displaystyle N} − число витков, i{displaystyle i} − ток в амперах , l{displaystyle l} − длина катушки в метрах и n{displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{displaystyle B} , умноженному на площадь поперечного сечения S{displaystyle S} и число витков N{displaystyle N}:

Ψ=μN2iSl=μn2iV,{displaystyle displaystyle Psi =mu _{0}N^{2}iS/l=mu _{0}n^{2}iV,}

где V=Sl{displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

L=μN2Sl=μn2V.{displaystyle displaystyle L=mu _{0}N^{2}S/l=mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным сердечником, то индуктивность отличается на множитель μ{displaystyle mu } — относительную магнитную проницаемость сердечника:

L=μμN2Sl=μμn2V.{displaystyle displaystyle L=mu _{0}mu N^{2}S/l=mu _{0}mu n^{2}V.}

В случае, когда μ>>1{displaystyle mu >>1}, под S

можно понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

• сглаживание пульсаций и помех, накопление энергии;
• создание магнитных полей в различных устройствах;
• фильтры цепей обратной связи;
• создание колебательных контуров;
• трансформаторы (устройство из двух катушек, связанных индуктивно);
• силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
• ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
• применение катушек в качестве электромагнитов различных исполнительных механизмов;
• обмотки электромагнитных реле;
• индукционные печи;
• установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

L = N х F : I.

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Тороидальная катушка (катушка с кольцевым сердечником)

Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:

где r – усредненный радиус тороидального сердечника.

Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:

где:

r – внутренний радиус сердечника;

R – внешний радиус;

Важно! Вторая формула позволяет узнавать результат с большей точностью.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ – магнитная постоянная, μ = 4π•10-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

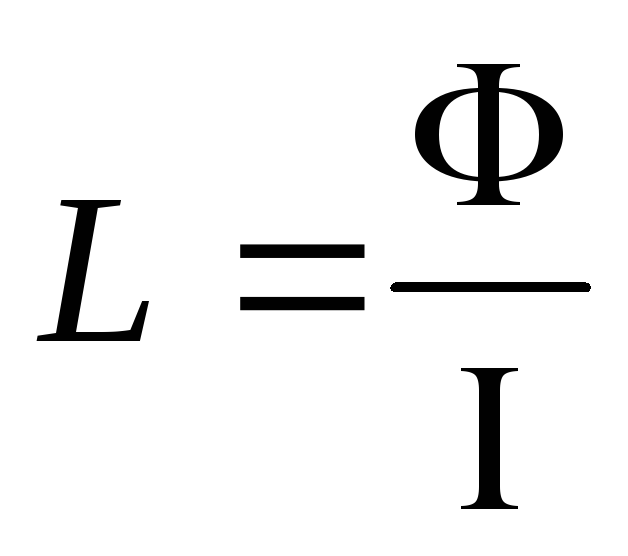
На постоянном токе

На частоте 50 кГц

Свойства

Имеет следующие свойства:

• Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
• Не может быть отрицательной;
• Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
• При увеличении частоты тока реактивное сопротивление катушки увеличивается;
• Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивное сопротивление – как его найти

Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:

XL=2*П*v*L

Здесь употреблены следующие обозначения:

1. XL – рассматриваемая величина.
2. Символом «П» обозначено число Пи.
3. V представляет собой частоту.
4. L — это обозначение величины индуктивности.

Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».

Катушки с различными сердечниками

Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:

I = U / XL

I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.

Конфигурация магнитного поля катушки

Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.

При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.

Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.

Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.

Магнитное поле провода

К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.

Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.

При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.

Советуем изучить Антенна для автомагнитолы

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Вам это будет интересно Щупы для мультиметра

Индуктивность, ее единица си. Индуктивность длинного соленоида.

Индукти́вность

(или
коэффициент самоиндукции
) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность , краем которой является этот контур. .

—магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока :

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током :

.

Электрическая цепь и индуктивность

Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.

Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.

Дроссель

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Колебательный контур

Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.

Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.

Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Читайте также:  Что осталось от советских заводов магнитофонов — 5 самых популярных марок

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят

Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.

Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

Таким образом коэффициент С1 и индуктивность L составят