Устройство асинхронной машины

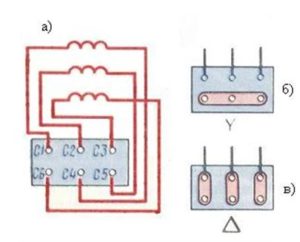
Схематичное устройство асинхронной машины

Классическая асинхронная машина состоит из 2 основных частей: ротора (подвижной) и статора (неподвижной). Три отдельные фазы составляют обмотку статора. С1, С2 и С3 — обозначения начала фаз. С3, С4 и С5 — соответственно концы фаз. Все они подсоединены к клеммному разъему по схеме звезда или треугольник, что показано на рисунках а, б, в. Схему выбирают учитывая паспортные данные двигателя и сетевое напряжение.

Статор создает внутри электродвигателя магнитное поле, которое постоянно вращается.

Ротор различают короткозамкнутый и фазный.

В короткозамкнутом скорость вращения не регулируется. Конструкция с ним проще и дешевле. Однако пусковой момент у него слишком мал по сравнению с машинами, у которых фазный ротор. Здесь скорость вращения регулируется за счет возможности ввода дополнительного сопротивления.

Принцип работы асинхронной машины

Подавая напряжение на обмотку статора, по каждой фазе можно наблюдать изменяющиеся магнитные потоки, которые по отношению друг к другу смещены на 120 градусов. Общий результирующий поток получается вращающимся и создает ЭДС внутри проводников ротора.

Там появляется ток, который во взаимодействии с результирующим потоком создает пусковой момент. Это приводит к вращению ротора.

Возникает скольжение S, т. е. разность между частотой вращения самого ротора n2 и частотой магнитного поля статора n1. Первоначально оно равно 1. Впоследствии частота возрастает, разность n1 – n2 уменьшается. Это ведет к уменьшению вращающего момента.

На холостом ходу скольжение минимально. Оно достигает критического значения Sкр, когда увеличивается статический момент. Превышение Sкр ведет к нестабильной работе машины.

Механические характеристики асинхронного двигателя

Механические характеристики асинхронного двигателя

— зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу).

Электромагнитный момент М, развиваемый асинхронным двигателем, можно определять двумя способами: через электромагнитную мощность Рэм и через полную механическую мощность двигателя Р2:

М=Р2’/ω, (39)

где Р2 —полная механическая мощность, Вт; ω=2πn/60 — механическая угловая скорость вращения ротора, 1/с; n — частота вращения ротора, об/мин.

Скорость ω связана с синхронной ω1 соотношением

Читайте также:  Эковатт: Определение внутреннего сопротивления генератора

Подставляя выражение для ω и Р2′ по уравнению (36) в уравнение (39), получаем

(40)

Выражение для момента через электромагнитную мощность имеет вид

М=Рэм/ω1,

Значение Рэм находится по уравнению (35), после чего представляем

Таким образом мы получим тождественное выражение для момента. Поскольку независимой величиной является не ток, а приложенное напряжение, то для получения окончательного выражения момента подставим в (40) значение тока I2′ по уравнению (32):

(41)

где М — момент, Н∙м; ω1 — синхронная скорость, с-1; U1 — напряжение, В; r1, r2′, x1, x2′ —сопротивления, Ом; s — скольжение, отн. ед.

Если необходимо иметь значение момента во внесистемных единицах — в килограммах силы-метрах, то полученный по (41) результат следует разделить на 9,81.

При эксплуатации часто необходимо определять момент по известной механической мощности Р2 (кВт) и частоте вращения n (об/мин). В этом случае формула (39) имеет вид, Н/м,

(42)

Отсюда мощность Р2 связана с моментом и частотой вращения соотношением

(43)

где М — момент, Н∙м; n — частота вращения, об/мин.

Если момент выражен в килограммах силы-метрах, то формулы (42), (43) преобразуются к виду

Читайте также:  Схема подключения 3-фазного реле контроля напряжения для дома

Зависимость между моментом и скольжением (41) при постоянном напряжении U1 и частоте f1 сети называется механической характеристикой. Естественная механическая характеристика асинхронного двигателя

приведена на рис. 20. Там же приведена механическая характеристика M=f (n), часто встречающаяся на практике и полученная из характеристики M = φ(s) пересчетом (s=0 соответствует синхронной частоте вращения n1, s =1-n=0 и т. д.).

Рис. 20. Естественная механическая характеристика асинхронного двигателя: a —M=f(s); б – n =f(М); А—генераторный режим; Б — режим двигателя; В — режим электромагнитного тормоза

Используя формулу (41), можно получить достаточно полное представление о механических характеристиках асинхронного двигателя

. Обратим прежде всего внимание на то, что механический момент двигателя зависит от трех групп величин: во-первых, это величины, определяемые конструкцией двигателя, к их числу относятся r1 и r’2, x1, х’2; во-вторых, величины, характеризующие напряжение, подводимое к двигателю, — напряжение на его зажимах U и частота питающего напряжения f (так как ω1 = 2πf); наконец, последняя величина, определяющая момент, развиваемый двигателем, зависит от режима его работы — это скольжение s.

Рассмотрим физические явления, обусловливающие такую форму механической характеристики. При частоте вращения ротора, равной синхронной, проводники ротора движутся с той же скоростью, что и вращающееся магнитное поле. Поэтому ЭДС, а следовательно, и ток в роторе равны нулю. Поэтому равен нулю и вращающий момент двигателя. При уменьшении частоты вращения ротора ниже синхронной проводники обмотки ротора начинают пересекать магнитное поле машины, в результате чего в обмотке ротора наводится ЭДС, пропорциональная скольжению ротора [см. формулу (14)]. При малых скольжениях (в пределах от s=0 до s=sкр) ток ротора также изменяется почти пропорционально скольжению. К такому выводу можно прийти, рассматривая уравнение (25) или (32). Так, в уравнении (25) при малых значениях s можно пренебречь составляющей sx2 в знаменателе по сравнению со значением r2, а в (32) можно пренебречь всеми составляющими в знаменателе по сравнению со значением r’2/s.

Таким образом, ток ротора в этом диапазоне скольжений практически определяется величиной ЭДС ротора, деленной на постоянное активное сопротивление r2 [уравнение (25)].

Как видно из рис. 20, механическая характеристика

в зоне малых скольжений sкр линейна. В этой же области скольжений находится и номинальное скольжение sном=0,01—0,1 (большие значения номинального скольжения относятся к двигателям мощностью до 1 кВт).

По мере увеличения скольжения увеличивается частота токов в роторе и возрастает влияние на характеристику индуктивного сопротивления ротора. Изменение тока, определяемое в зоне малых скольжений в основном активным сопротивлением [см. формулу (25)], замедляется, и при некотором скольжении, называемом критическим sкр, достигается максимальное значение момента. При дальнейшем увеличении скольжения (уменьшении частоты вращения ротора) момент будет уменьшаться.

Критическое скольжение находится по формуле

(44)

где знак плюс соответствует двигательному режиму работы, а минус — генераторному (как следует из рис. 20, генераторный режим соответствует области отрицательных скольжений).

Поскольку для двигателей мощностью более 1 кВт практически всегда r1<<(х1 + х’2), то формулу для критического скольжения можно упростить:

(44а)

Теперь, подставляя значение s=sкр в формулу (41), получим выражение для максимального момента

(45)

Взяв теперь отношение текущего значения момента к максимальному М/Мmax при условии r1≈0, получим

(46)

Формула (46) оказывается весьма удобной, так как позволяет построить механическую характеристику двигателя M=f(s) при известных значениях максимального момента и соответствующего ему критического скольжения. Задавая текущее значение скольжения в диапазоне 0max=f (s).

Относительный максимальный момент определяет его перегрузочную способность, т. е. способность двигателя кратковременно выдерживать нагрузки, большие номинальной. В электрических машинах перегрузочная способность обозначает kм и определяется как

kм = Mmax/Mном (47)

Важное значение имеет пусковой момент, который можно рассчитывать по общей формуле (41) при подстановке в нее s= 1:

(48)

Относительное значение пускового момента kп определяет способность двигателя разгоняться до рабочей частоты вращения с полной нагрузкой на валу и определяется как

Читайте также:  Самостоятельная настройка антенны на спутник НТВ+. НТВ+Восток (Экспресс АТ1), НТВ+Дальний Восток (Экспресс АТ2)

kп = Mп/Mном

В ряде случаев вместо (46) удобнее пользоваться формулой, в которой текущий момент двигателя отнесен не к максимальному, а к номинальному моменту. В этом случае

(49)

где sкр, sном — значения критического и номинального скольжения двигателя; ρ=r1/r’2 (для двигателей серии 4А с высотой оси вращения 56—132 мм пользуются значением ρ≈1,32).

Если пренебречь величиной r1 (т. е. положить ρ=0), то из (49) следует

(50)

Анализ выражения (41) для электромагнитного момента показывает, чт момент зависит от квадрата напряжения сети, что является недостатком асинхронных двигателей. Так, при снижении напряжения на 10 % момент уменьшается на 19%, а при снижении напряжения на 20 % уменьшение момента составляет 36%. На рис. 21 изображены механические характеристики двигателя при номинальном питающем напряжении (естественная характеристика) и при пониженном напряжении.

При уменьшении напряжения, питающего двигатель, который работает под нагрузкой, его вращающий момент снижается. В результате этого происходит снижение частоты вращения двигателя. Частота снижается (и соответственно увеличивается скольжение) до тех пор, пока вращающий момент двигателя не станет равным статическому моменту сопротивления Мс, обусловленному (приводом (соответствующие частоты вращения показаны точками на механических характеристиках рис. 21). При сильном уменьшении напряжения может случиться, что максимальный момент окажется меньше момента сопротивления Мс. В этом случае двигатель опрокидывается, т. е. его частота вращения уменьшается и в конце концов он останавливается. При заторможенном роторе по обмоткам двигателя протекают большие токи, и во избежание аварии сам двигатель должен быть отключен от сети (эти функции выполняет тепловая защита).

Рис. 21. Механические характеристики асинхронного двигателя при различных значениях питающего напряжения

Механическая характеристика

Как основная, помогает проводить детальный анализ работы электродвигателя. Она выражает непосредственную зависимость частоты вращения самого ротора от электромагнитного момента n=f (M).

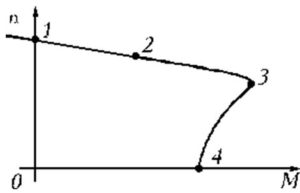
Из графика видно, что на участке 1-3 машина работает устойчиво. 3-4 — непосредственный отрезок неустойчивой работы. Идеальный холостой ход соответствует точке 1.

Точка 2 — номинальный режим работы. Точка 3 — частота вращения достигла критического значения. Пусковой момент Мпуск — точка 4.

Наши читатели рекомендуют! Для экономии на платежах за электроэнергию наши читатели советуют ‘Экономитель энергии Electricity Saving Box’. Ежемесячные платежи станут на 30-50% меньше, чем были до использования экономителя. Он убирает реактивную составляющую из сети, в результате чего снижается нагрузка и, как следствие, ток потребления. Электроприборы потребляют меньше электроэнергии, снижаются затраты на ее оплату.

Существуют технические способы расчетов и построения механической характеристики с учетом данных паспорта.

В первоначальной точке 1 n0=60f/p (p – количество пар полюсов). Поскольку nн и Mн непосредственно координаты точки 2, расчет номинального момента производится по формуле Mн=9,55*Рн/ nн, где Рн — номинальная мощность. Значение nн указано в паспорте двигателя. В точке 3 Mкр=Mнλ. Пусковой момент в точке 4 Mпуск=Mн*λпуск (значения λ, λпуск — из паспорта).

Механическая характеристика, построенная таким образом, называется естественной. Изменяя другие параметры можно получить искусственную механическую характеристику.

Полученные результаты дают возможность проанализировать и согласовать механические свойства самого двигателя и рабочего механизма.

Электромеханическая характеристика

Она являет собой зависимость угловой скорости вращения от тока статора. Используя несколько опорных точек можно построить электромеханическую характеристику. Номинальный ток рассчитывается по формуле:

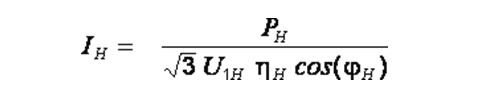
Ток холостого хода составляет 30—40% от номинального.

Формула расчета при критическом скольжении:

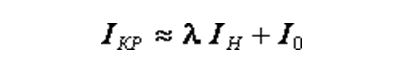
Ток в начальный момент пуска:

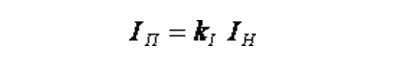
Все значения отражают электромеханическую характеристику.